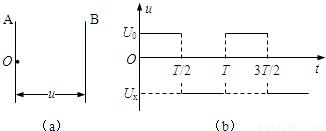
题目内容
如图a所示，为一组间距d足够大的平行金属板，板间加有随时间变化的电压（如图b所示），设U和T已知．A板上O处有一静止的带电粒子，其带电量为q，质量为m（不计重力），在t=0时刻起该带电粒子受板间电场加速向B板运动，途中由于电场反向，粒子又向A板返回（粒子未曾与B板相碰）．（1）当Ux=2U时求带电粒子在t=T时刻的动能；
（2）为使带电粒子在0～T时间内能回到O点，Ux要大于多少？
【答案】分析：（1）粒子前半个周期加向右速运动，后半个周期，先向右减速运动，速度减至零时，向左加速运动，将后半个周期内的运动看成一种有往复有匀减速运动，由牛顿第二定律求出粒子匀加速和匀减速运动的加速度大小，由速度公式可求得求出t=T时刻的速度，即可求出动能．
（2）由位移公式分别求出前个周期内和后装修周期内位移的表达式，粒子回到O点时，两个位移大小相等、方向相反，联立解得Ux．
解答：解：（1）粒子在前半个周期内加速度为：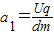
，在后半个周期内加速度为：
，
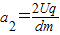t=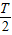
时刻粒子的速度为：
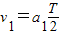，将后半个周期内的运动看成一种有往复有匀减速运动，则有：
，
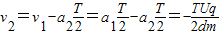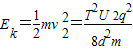
（2）粒子在前半个周期内位移为：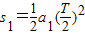
，在后半个周期内位移为：
，
，
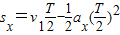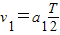为使带电粒子在0～T时间内能回到O点，则有：s1=-sx，
联立上面各式，得：ax=3a1，
因为：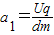
，
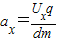，所以：Ux=3U．
答：（1）当Ux=2U时求带电粒子在t=T时刻的动能为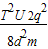
；
（2）为使带电粒子在0～T时间内能回到O点，Ux要大于3U．
点评：本题首先要分析粒子的运动情况，再选择解题规律，技巧是将往复运动看成一种匀减速运动，要抓住两个过程之间的关系，比如速度关系和位移关系等，进行分析．
（2）由位移公式分别求出前个周期内和后装修周期内位移的表达式，粒子回到O点时，两个位移大小相等、方向相反，联立解得Ux．
解答：解：（1）粒子在前半个周期内加速度为：
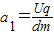，在后半个周期内加速度为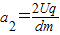：，t=
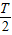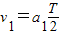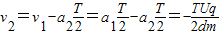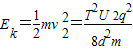
时刻粒子的速度为：，将后半个周期内的运动看成一种有往复有匀减速运动，则有：，（2）粒子在前半个周期内位移为：
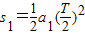，在后半个周期内位移为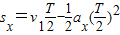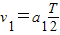：，，为使带电粒子在0～T时间内能回到O点，则有：s1=-sx，
联立上面各式，得：ax=3a1，
因为：
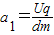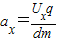，，所以：Ux=3U．答：（1）当Ux=2U时求带电粒子在t=T时刻的动能为
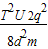；（2）为使带电粒子在0～T时间内能回到O点，Ux要大于3U．
点评：本题首先要分析粒子的运动情况，再选择解题规律，技巧是将往复运动看成一种匀减速运动，要抓住两个过程之间的关系，比如速度关系和位移关系等，进行分析．
练习册系列答案
阅读快车系列答案
相关题目
如图a所示，为一组间距d足够大的平行金属板，板间加有随时间变化的电压（如图b所示），设U0和T已知．A板上O处有一静止的带电粒子，其带电量为q，质量为m（不计重力），在t=0时刻起该带电粒子受板间电场加速向B板运动，途中由于电场反向，粒子又向A板返回（粒子未曾与B板相碰）．
