Question

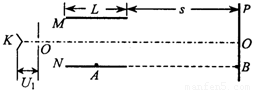
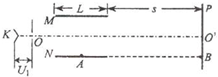真空室中有如图所示的装置，设电子电量为e、质量为m．电极K发出的电子（初速不计）经过加速电场后，由小孔O沿水平放置的偏转板M、N间的中心轴线OO'射入．M、N板长为L，两板间的距离d，两板间加有恒定电压U₂，它们间的电场可看作匀强电场．偏转板右端边缘到荧光屏P的距离为s．当加速电压为U₁时，电子恰好打在荧光屏的B点．已知A、B点到中心轴线OO′的距离相等．求U₁．

Answer 1

分析：（1）粒子在加速电场中，电场力做功，由动能定理求出速度v₀．
（2）粒子进入偏转电场后，做类平抛运动，运用运动的合成与分解求出电压．

解答：解：由题意，电子在偏转电场中做类平抛运动．设电子进入偏转电场时的速度为v：eU1=

1

2

mv2
偏转距离为y₂，沿板方向的位移为L=vt
y2=

1

2

at2
a=

eU2

md

如图，电子从C点离开电场，沿直线CB匀速运动打在B点
由几何关系得

y1-y2

S

=

at

v

y₁=

1

2

d
由以上各式解得U1=

U2L(s- L 2 )

d2

答：偏转电场的电压：U1=

U2L(s- L 2 )

d2

点评：本题考查了带电粒子在电场中加速和偏转问题，注意带电粒子在偏转电场中做类平抛运动，根据平抛运动的基本规律解题．