题目内容
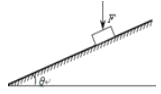
【题目】一个质量m=2kg的滑块在倾角为θ=37°的固定斜面上，受到一个大小为40N的水平推力F作用，以v0=10m/s的速度沿斜面匀速上滑．（sin37°=0.6，取g=10m/s2）
（1）求滑块与斜面间的动摩擦因数；
（2）若滑块运动到A点时立即撤去推力F，求这以后滑块再返回A点经过的时间．
【答案】
（1）
解：滑块在水平推力作用下沿斜面向上匀速运动时，合力为零，则有
Fcos37°=mgsin37°+μ（mgcos37°+Fsin37°）
代入解得，μ=0.5
（2）
解：撤去F后，滑块上滑过程：
根据牛顿第二定律得：mgsin37°+μmgcos37°=ma1，
得，a1=g（sin37°+μcos37°）
上滑的时间为 t1= 
=1s
上滑的位移为 x= 
=5m
滑块下滑过程：mgsin37°﹣μmgcos37°=ma2，
得，a2=g（sin37°﹣μcos37°）
由于下滑与上滑的位移大小相等，则有
x= 
解得， 
= 
s
故 t=t1+t2=（1+ ）s
【解析】（1）滑块在水平推力作用下沿斜面向上匀速运动，合力为零，根据正交分解法列方程，求解动摩擦因数；（2）若滑块运动到A点时立即撤去推力F，滑块先向上做匀减速运动，后向下做匀加速运动．根据牛顿第二定律和运动学公式结合求解时间．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
