题目内容
 如图所示,在xoy坐标系中分布着三个有界场区:第一象限中有一半径为r=0.1m的圆形磁场区域,磁感应强度B1=1T,方向垂直纸面向里,该区域同时与x轴、y轴相切,切点分别为A、C;第四象限中,由y轴、抛物线FG(y=-10x2+x-0.025,单位:m)和直线DH( y=x-0.425,单位:m)构成的区域中,存在着方向竖直向下、强度E=2.5N/C的匀强电场;以及直线DH右下方存在垂直纸面向里的匀强磁场B2=0.5T.现有大量质量为1×10-6kg(重力不计),电量大小为2×10-4C,速率均为20m/s的带负电的粒子从A处垂直磁场进入第一象限,速度方向与y轴夹角在0至180度之间.
如图所示,在xoy坐标系中分布着三个有界场区:第一象限中有一半径为r=0.1m的圆形磁场区域,磁感应强度B1=1T,方向垂直纸面向里,该区域同时与x轴、y轴相切,切点分别为A、C;第四象限中,由y轴、抛物线FG(y=-10x2+x-0.025,单位:m)和直线DH( y=x-0.425,单位:m)构成的区域中,存在着方向竖直向下、强度E=2.5N/C的匀强电场;以及直线DH右下方存在垂直纸面向里的匀强磁场B2=0.5T.现有大量质量为1×10-6kg(重力不计),电量大小为2×10-4C,速率均为20m/s的带负电的粒子从A处垂直磁场进入第一象限,速度方向与y轴夹角在0至180度之间.(1)求这些粒子在圆形磁场区域中运动的半径;
(2)试证明这些粒子经过x轴时速度方向均与x轴垂直;
(3)通过计算说明这些粒子会经过y轴上的同一点,并求出该点坐标.
【答案】分析:(1)根据带电粒子在匀强磁场中运动的半径公式求出粒子运动的半径.
(2)粒子在匀强磁场中做圆周运动的半径与圆形磁场区域的半径相等,通过速度方向与圆周运动的轨道半径垂直,结合几何关系进行证明.
(3)粒子离开圆形磁场沿电场线方向进入电场,速度方向与电场方向一致,根据动能定理得出进入磁场的速度,通过抛物线和直线的轨迹方程,结合圆周运动的知识求出粒子打到y轴上的坐标.
解答:解:(1)根据B1qv= 得
得
R1= =0.1m
=0.1m
(2)考察从A点以任意方向进入磁场的粒子,设其从K点离开磁场,O1和O2分别是磁场区域和圆周运动的圆心,因为圆周运动半径和磁场区域半径相同,因此O1AO2K为菱形,离开磁场时速度垂直于O2K,即垂直于x轴,
得证.
(3)设粒子在第四象限进入电场时的坐标为(x,y1),离开电场时的坐标为(x,y2),离开电场时速度为v2,在B2磁场区域做圆周运动的半径为R2.
有Eq(y2-y1)=
 -
- mv2
mv2
B2qv2=
并将y1=-10x2+x-0.025和y2=x-0.425代入得R2=X 因v2的方向与DH成45°,且半径刚好为x坐标值,则粒子做圆周运动的圆心必在y轴上,在此磁场中恰好经过四分之一圆周,并且刚好到达H处,H点坐标为(0,-0.425).
答:(1)这些粒子在圆形磁场区域中运动的半径为0.1m.
(2)证明如上.
(3)该点坐标为(0,-0.425).
点评:本题考查了带电粒子在电场和磁场中的运动,关键理清粒子的运动的过程,结合动能定理,牛顿第二定律等知识进行求解,本题对数学能力的要求较高.
(2)粒子在匀强磁场中做圆周运动的半径与圆形磁场区域的半径相等,通过速度方向与圆周运动的轨道半径垂直,结合几何关系进行证明.
(3)粒子离开圆形磁场沿电场线方向进入电场,速度方向与电场方向一致,根据动能定理得出进入磁场的速度,通过抛物线和直线的轨迹方程,结合圆周运动的知识求出粒子打到y轴上的坐标.
解答:解:(1)根据B1qv=
 得
得
R1=
 =0.1m
=0.1m (2)考察从A点以任意方向进入磁场的粒子,设其从K点离开磁场,O1和O2分别是磁场区域和圆周运动的圆心,因为圆周运动半径和磁场区域半径相同,因此O1AO2K为菱形,离开磁场时速度垂直于O2K,即垂直于x轴,
得证.
(3)设粒子在第四象限进入电场时的坐标为(x,y1),离开电场时的坐标为(x,y2),离开电场时速度为v2,在B2磁场区域做圆周运动的半径为R2.
有Eq(y2-y1)=

 -
- mv2
mv2 B2qv2=

并将y1=-10x2+x-0.025和y2=x-0.425代入得R2=X 因v2的方向与DH成45°,且半径刚好为x坐标值,则粒子做圆周运动的圆心必在y轴上,在此磁场中恰好经过四分之一圆周,并且刚好到达H处,H点坐标为(0,-0.425).
答:(1)这些粒子在圆形磁场区域中运动的半径为0.1m.
(2)证明如上.
(3)该点坐标为(0,-0.425).
点评:本题考查了带电粒子在电场和磁场中的运动,关键理清粒子的运动的过程,结合动能定理,牛顿第二定律等知识进行求解,本题对数学能力的要求较高.

练习册系列答案
相关题目
 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2) 如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求:
如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求: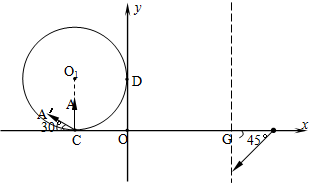 D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
