题目内容
（18分）如图所示，传送带长L=7m，与水平成
=37°角，以
沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为
，当物块滑到底端时，有一质量为m=0.01kg的子弹以
原速度射入物块，后又以
的速度穿出物块，以后每隔
就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）
（1）求物块滑到传送带底端时速度；
（2）通过计算说明物块滑离传送带时，有几颗子弹穿过物块；
（1）
（2）有三颗子弹穿过物体
解析:（1）开始下滑时摩擦力沿斜面向下，由牛顿第二定律可得
…………1分
则
…………1分
物块加速到速度为
时摩擦力沿斜面向上，
所用时间
…………1分
这一过程中物块的位移
…………1分
此后，根据牛顿第二定律：
…………1分
得：
…………1分
设物块滑到底端时的速度为v1，
由公式
…………1分
得 …………1分
（2）第一颗子弹射入物块，由动量守恒可得
…………1分
得
…………1分
由于物块上滑的加速度为a1，其速度减速到零的时间为
所以物块上滑的位移为
…………1分
然后物块下滑，经时间
与第二颗子弹相遇，相遇瞬时，物块速度为
下滑位移为
…………2分
第二颗子弹射入物块，有
…………1分
物块向上减速0.73s时的速度为
此过程位移
…………1分
此时物块离顶端距离为
…………1分
第三颗子弹射入物块，有
…………1分
由于此后物体减速至零的位移
故有三颗子弹穿过物体 …………1分
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
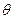=37°角，以
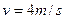沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为
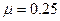，当物块滑到底端时，有一质量为m=0.01kg的子弹以
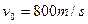原速度射入物块，后又以
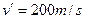的速度穿出物块，以后每隔
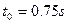就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）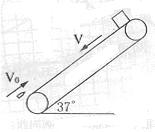
=37°角，以
沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为
，当物块滑到底端时，有一质量为m=0.01kg的子弹以
原速度射入物块，后又以
的速度穿出物块，以后每隔
就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）
=37°角，以
沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为
，当物块滑到底端时，有一质量为m=0.01kg的子弹以
原速度射入物块，后又以
的速度穿出物块，以后每隔
就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）