题目内容
18.在匀强磁场中有一个静止放置的放射性元素的原子核,当它放出一个α粒子后,它们的速度方向都与磁场方向垂直.若测得α粒子和反冲核的轨道半径之比为44:1,则反冲核的电荷数是多少?分析 核衰变过程动量守恒,反冲核与释放出的粒子的动量大小相等,结合带电粒子在匀强磁场中圆周运动的半径公式可得小粒子与反冲核的电荷量之比,从而得到反冲核的电荷数.
解答 解:放射性元素的原子核,放出α粒子的过程动量守恒,由于初始动量为零,所以末态动量也为零,即α粒子和反冲核的动量大小相等、方向相反,即p1=p2=p
α粒子和反冲核在磁场中均做匀速圆周运动,由洛伦兹力提供向心力,得
qvB=m$\frac{{v}^{2}}{R}$
解得 R=$\frac{mv}{qB}$
所以α粒子的半径:R1=$\frac{p}{2eB}$
设反冲核的电荷量为Q,则反冲核的半径:
R2=$\frac{p}{QB}$
所以:$\frac{{R}_{1}}{{R}_{2}}$=$\frac{Q}{2e}$=$\frac{44}{1}$,Q=88e.
即反冲核的电荷数是88.
答:反冲核的电荷数是88.
点评 原子核的衰变过程类比于爆炸过程,满足动量守恒,而带电粒子在匀强磁场中圆周运动的半径公式R=$\frac{mv}{qB}$中的分子恰好是动量的表达式,要巧妙应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
9.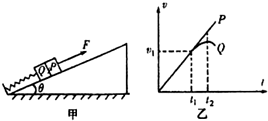 如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
 如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )
如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则( )| A. | 施加拉力前,Q给P的力大小为mgsinθ | |
| B. | 施加拉力前,弹簧的形变量为$\frac{2mgsinθ}{k}$ | |
| C. | 到t1时刻,弹簧释放的弹性势能为$\frac{1}{2}$mv12 | |
| D. | t2时刻弹簧恢复到原长,物块Q达到速度最大值 |
3. 如图所示,河水的流速为v=8m/s,一条船要从河的南岸A点沿与河岸成37°角的直线航行判北岸下游某处,则船的开行速度(相对于承的速度)最小为(sin37°=0.6,cos37°=0.8)( )
如图所示,河水的流速为v=8m/s,一条船要从河的南岸A点沿与河岸成37°角的直线航行判北岸下游某处,则船的开行速度(相对于承的速度)最小为(sin37°=0.6,cos37°=0.8)( )
 如图所示,河水的流速为v=8m/s,一条船要从河的南岸A点沿与河岸成37°角的直线航行判北岸下游某处,则船的开行速度(相对于承的速度)最小为(sin37°=0.6,cos37°=0.8)( )
如图所示,河水的流速为v=8m/s,一条船要从河的南岸A点沿与河岸成37°角的直线航行判北岸下游某处,则船的开行速度(相对于承的速度)最小为(sin37°=0.6,cos37°=0.8)( )| A. | 4m/s | B. | 4.8m/s | C. | 6mn/s | D. | 8m/s |
18.甲、乙两球质量不同,M甲>M乙,它们从同一高度同时自由下落(不考虑空气阻力),则下列说法正确的是 ( )
| A. | 甲比乙先落地 | B. | 乙比甲先落地 | ||
| C. | 甲、乙同时落地 | D. | 无法判断谁先落地 |
 “霾”主要指原因不明的因大量烟、尘等微粒悬浮而形成的浑浊现象.根据目前的认识,机动车尾气排放、煤炭燃烧和工业生产的燃烧过程中排放的二氧化硫和氮氧化物等是产生霾的主要来源.它会对人的呼吸系统、神经系统等产生影响.将火车由燃烧汽油、柴油等改为使用电力,是从源头减少“霾”的重要措施.高铁列车采用动力分散的电力机车驱动方式.国家电网将220kV高压电送至高铁牵引站,经牵引站变压后送达接触网.铁路沿线上方悬挂着的金属线就是接触网.接触网额定电压为25kV.车顶伸出的“长辫子”般的受电弓与接触网滑动接触获得电能而牵引列车运行.假设列车由18节车厢组成,除第1、18节两车厢为无动力车厢外,其余16节车厢均装备动力系统,各动力车厢产生的动力相同,每节车厢(含乘客行李等)的平均质量均为10吨.假设运动时每节车厢所受的阻力恒为车重的$\frac{1}{36}$倍,该列车匀加速启动时,能在800s内将速度提升到360公里每小时,此后列车保持恒定功率,列车达到最大速度后匀速运动.(g取10m/s2.)求:
“霾”主要指原因不明的因大量烟、尘等微粒悬浮而形成的浑浊现象.根据目前的认识,机动车尾气排放、煤炭燃烧和工业生产的燃烧过程中排放的二氧化硫和氮氧化物等是产生霾的主要来源.它会对人的呼吸系统、神经系统等产生影响.将火车由燃烧汽油、柴油等改为使用电力,是从源头减少“霾”的重要措施.高铁列车采用动力分散的电力机车驱动方式.国家电网将220kV高压电送至高铁牵引站,经牵引站变压后送达接触网.铁路沿线上方悬挂着的金属线就是接触网.接触网额定电压为25kV.车顶伸出的“长辫子”般的受电弓与接触网滑动接触获得电能而牵引列车运行.假设列车由18节车厢组成,除第1、18节两车厢为无动力车厢外,其余16节车厢均装备动力系统,各动力车厢产生的动力相同,每节车厢(含乘客行李等)的平均质量均为10吨.假设运动时每节车厢所受的阻力恒为车重的$\frac{1}{36}$倍,该列车匀加速启动时,能在800s内将速度提升到360公里每小时,此后列车保持恒定功率,列车达到最大速度后匀速运动.(g取10m/s2.)求: :量程0~200μA,内阻500Ω
:量程0~200μA,内阻500Ω 改装成一个量程略大于2.5V的伏特表,将改装的电路图画在图甲的方框内,此伏特表
改装成一个量程略大于2.5V的伏特表,将改装的电路图画在图甲的方框内,此伏特表 的量程是2.6V(本问结果取两位有效数字);
的量程是2.6V(本问结果取两位有效数字); 和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线
和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线 的示数为1.5V,则通过小灯泡的电流强度为0.25A
的示数为1.5V,则通过小灯泡的电流强度为0.25A
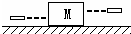 质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图设子弹均未射穿木块,子弹质量为m(M=2m)且两颗子弹与木块之间的作用力大小均相同.,求:当两颗子弹均相对木块静止时d1与 d2的比值.
质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图设子弹均未射穿木块,子弹质量为m(M=2m)且两颗子弹与木块之间的作用力大小均相同.,求:当两颗子弹均相对木块静止时d1与 d2的比值. 光滑活塞封闭气缸内一定体积的气体,气缸静止在水平面上.已知活塞的质量为m、横截面积为s,气缸的质量为M,被封闭气体的高度为h1.然后用力(大小未知)缓慢向上提拉活塞,气缸刚离开地面时气体的高度为h2.已知重力加速度为g,不考虑被封闭气体的质量,求当地的大气压强.
光滑活塞封闭气缸内一定体积的气体,气缸静止在水平面上.已知活塞的质量为m、横截面积为s,气缸的质量为M,被封闭气体的高度为h1.然后用力(大小未知)缓慢向上提拉活塞,气缸刚离开地面时气体的高度为h2.已知重力加速度为g,不考虑被封闭气体的质量,求当地的大气压强.