Question

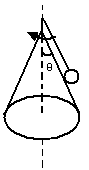
如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球．圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面，此时绳的张力是多少？若要小球离开锥面，则小球的角速度至少为多少？

Answer 1

答案：
解析：

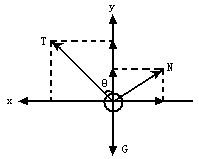
巧解导析：小球以圆锥轴线为轴，在水平面内匀速转动，要小球离开锥面的临界条件是锥面对小球的弹力为零． 　　解答：(1)对小球进行受力分析，如图所示，根据牛顿第二定律，x方向上有     　　　　    　　　　　　　　    T·sinθ－N·cosθ＝mω2r， y方向上有 　　　　　　　　　　 N·sinθ＋T·cosθ－G＝0， 又因r＝L·sinθ并列可得 　　　　　　　　    T＝mgcosθ＋mω2Lsin2θ． 　　(2)当小球刚好离开锥面时N＝0(临界条件)，则有： 　　　　　　    Tsinθ＝mω2r，  Tcosθ－G＝0， 解得　　　　　　　　　　　　　　 ω＝． 即小球的角速度至少为才可使小球离开锥面．

提示：

当小球和圆锥一起匀速转动时，找准小球的半径和圆心．当小球要离开锥面时，找到其临界条件．