题目内容
质量为m的球放在光滑的倾角为θ的斜面上,被竖直挡板挡住,求它对竖直板的压力以及对斜面的压力.
【答案】分析:以球为研究对象并进行受力分析,F为斜面对球的支持力,FN为竖直板对球的支持力,根据球平衡的条件则有
cosθ=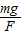 ,和tanθ=
,和tanθ=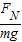 即可求得球对斜面的压力和对竖直板的压力.
即可求得球对斜面的压力和对竖直板的压力.
解答: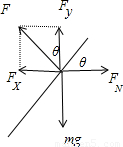 解:以球为研究对象并进行受力分析,F为斜面对球的支持力,FN为竖直板对球的支持力,如图所示,
解:以球为研究对象并进行受力分析,F为斜面对球的支持力,FN为竖直板对球的支持力,如图所示,
则有cosθ=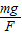 ,
,
故F=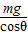 ,
,
根据牛顿第三定律可得球对斜面的压力等于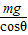 ,
,
又tanθ=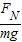 ,则FN=mgtanθ,
,则FN=mgtanθ,
根据牛顿第三定律可得球对竖直板的压力等于mgtanθ.
答:球对竖直板的压力等于mgtanθ,对斜面的压力等于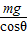 .
.
点评:在解答本题的时候很多同学容易忘记题目是让我们求球对竖直板和球对斜面的压力,而我们求解的是竖直板和斜面对球的作用力,故需要根据牛顿第三定律求出球对竖直板的压力以及对斜面的压力.
cosθ=
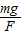 ,和tanθ=
,和tanθ=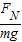 即可求得球对斜面的压力和对竖直板的压力.
即可求得球对斜面的压力和对竖直板的压力.解答:
 解:以球为研究对象并进行受力分析,F为斜面对球的支持力,FN为竖直板对球的支持力,如图所示,
解:以球为研究对象并进行受力分析,F为斜面对球的支持力,FN为竖直板对球的支持力,如图所示,则有cosθ=
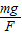 ,
,故F=
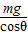 ,
,根据牛顿第三定律可得球对斜面的压力等于
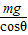 ,
,又tanθ=
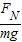 ,则FN=mgtanθ,
,则FN=mgtanθ,根据牛顿第三定律可得球对竖直板的压力等于mgtanθ.
答:球对竖直板的压力等于mgtanθ,对斜面的压力等于
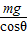 .
.点评:在解答本题的时候很多同学容易忘记题目是让我们求球对竖直板和球对斜面的压力,而我们求解的是竖直板和斜面对球的作用力,故需要根据牛顿第三定律求出球对竖直板的压力以及对斜面的压力.

练习册系列答案
相关题目