题目内容
有一物体以某一速度从斜面底沿斜面上滑，当它滑行4米后速度变为零，然后再下滑到斜面底．斜面倾斜角θ=37°，物体和斜面间的动摩擦因数μ=0.25．（已知：sin37°=0.6，cos37°=0.8，g=10m/s2．）求：（1）物体开始上滑时的速度vo；
（2）物体返回到斜面底时的速度vt．
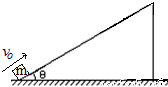
【答案】分析：本题可以运用动能定理求解，也可以利用牛顿运动定律求解，但利用动能定理求解简洁方便．
解答：解：（1）上滑过程由动能定理有：-mgLsinθ-µmgLcosθ=0-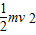
解得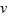
=8m/s
故物体开始上滑时的速度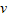
为8m/s．
（2）下滑过程由动能定理有：mgLsinθ-µmgLcosθ=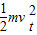
-0
vt=4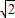
m/s=5.6m/s
故物体返回到斜面底时的速度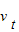
为5.6m/s．
点评：涉及到速度大小、位移大小、“功”、“动能”、多过程问题时要优先利用动能定理解决．
解答：解：（1）上滑过程由动能定理有：-mgLsinθ-µmgLcosθ=0-
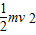
解得
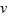=8m/s故物体开始上滑时的速度
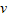为8m/s．（2）下滑过程由动能定理有：mgLsinθ-µmgLcosθ=
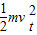-0 vt=4
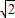m/s=5.6m/s故物体返回到斜面底时的速度
为5.6m/s．点评：涉及到速度大小、位移大小、“功”、“动能”、多过程问题时要优先利用动能定理解决．
练习册系列答案
相关题目
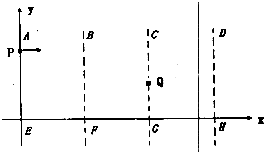如图所示，竖直平面xoy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG．三个区域中分别存在方向+y、+y、+x的匀强电场，其场强大小比例为2：1：2．现有一带正电的物体以某一初速度从坐标为（0，L）的P点射入ABFE场区，初速度方向水平向右．物体恰从坐标为（2L，
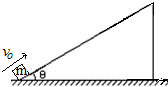有一物体以某一速度从斜面底沿斜面上滑，当它滑行4米后速度变为零，然后再下滑到斜面底．斜面倾斜角θ=37°，物体和斜面间的动摩擦因数μ=0.25．（已知：sin37°=0.6，cos37°=0.8，g=10m/s2．）求：
