题目内容
 如图所示,左边固定一个弧面光滑的四分之一圆槽,圆槽半径R=1m,其底端切线水平,质量为M=2kg的小车紧靠圆槽,放在光滑水平面上,它的上表面与圆槽底端等高,已知车长L=1m,一质量为m=1kg的滑块从圆槽弧面上h=0.8m高处由静止释放,滑块可视为质点,滑块与车的上表面之间的动摩擦因数为μ=0.5,(取g=10m/s2)求:
如图所示,左边固定一个弧面光滑的四分之一圆槽,圆槽半径R=1m,其底端切线水平,质量为M=2kg的小车紧靠圆槽,放在光滑水平面上,它的上表面与圆槽底端等高,已知车长L=1m,一质量为m=1kg的滑块从圆槽弧面上h=0.8m高处由静止释放,滑块可视为质点,滑块与车的上表面之间的动摩擦因数为μ=0.5,(取g=10m/s2)求:(1)滑块刚滑到圆槽底端O点时所受的支持力的大小;
(2)求滑块离开小车时的速度的大小.
分析:(1)滑块下滑过程,只有重力做功,机械能守恒,根据守恒定律列式求解O点速度;在O点,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力;
(2)滑块在小车上滑动过程,系统动量守恒,根据动量守恒定律列式;再由一定滑动摩擦力做的总功等于内能减小量并根据功能关系列式;最后联立求解.
(2)滑块在小车上滑动过程,系统动量守恒,根据动量守恒定律列式;再由一定滑动摩擦力做的总功等于内能减小量并根据功能关系列式;最后联立求解.
解答:解:(1)设滑块刚滑到圆槽底端O点时速度为v0
滑块下滑过程机械能守恒,有:
mgh=
m
①
在O点由牛顿第二定律有:
F支-mg=m
②
联立①②立得:F支=26N
(2)设滑块离开小车时的速度v,此时车速为v′,由动量守恒有:
mv0=mv+Mv′③
由功能关系,有:
m
-(
mv2+
Mv′2)=μmgL ④
由①③④解得:v=2m/s
答:(1)滑块刚滑到圆槽底端O点时所受的支持力的大小为26N;
(2)滑块离开小车时的速度的大小为2m/s.
滑块下滑过程机械能守恒,有:
mgh=
| 1 |
| 2 |
| v | 2 0 |
在O点由牛顿第二定律有:
F支-mg=m
| ||
| R |
联立①②立得:F支=26N
(2)设滑块离开小车时的速度v,此时车速为v′,由动量守恒有:
mv0=mv+Mv′③
由功能关系,有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
由①③④解得:v=2m/s
答:(1)滑块刚滑到圆槽底端O点时所受的支持力的大小为26N;
(2)滑块离开小车时的速度的大小为2m/s.
点评:本题第一问较为基础,根据机械能守恒定律和牛顿第二定律并结合向心力公式列式求解即可;第二问关键根据功能关系和动量守恒定律列式,如果采用牛顿第二定律与运动学公式相结合求解,会使问题复杂化.

练习册系列答案
相关题目
 如图所示,MN是一根固定的通电长直导线,电流方向向上,今将一金属线框放在导线上,让线框的位置偏向MN的左边,两者彼此绝缘,当MN中的电流突然增大时,线框整体受力情况为( )
如图所示,MN是一根固定的通电长直导线,电流方向向上,今将一金属线框放在导线上,让线框的位置偏向MN的左边,两者彼此绝缘,当MN中的电流突然增大时,线框整体受力情况为( )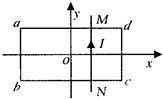 如图所示,MN是一根固定的通电直导线,电流方向由N到M.今将一金属线框abcd放在导线上,让线框的位置偏向导线的左边,两者彼此绝缘.当导线中的电流突然增大时,线框整体受力情况为( )
如图所示,MN是一根固定的通电直导线,电流方向由N到M.今将一金属线框abcd放在导线上,让线框的位置偏向导线的左边,两者彼此绝缘.当导线中的电流突然增大时,线框整体受力情况为( )
