题目内容
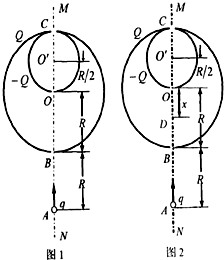
 如图所示,两个固定的均匀带电球面,所带电荷量分别为+Q和-Q (Q>0),半径分别为R和
如图所示,两个固定的均匀带电球面,所带电荷量分别为+Q和-Q (Q>0),半径分别为R和| R | 2 |
(1)要使质点从 A 点上抛后能够到达B点,所需的最小初动能为多少?
(2)要使质点从A点上抛后能够到达O点,在不同条件下所需的最小初动能各为多少?
分析:(1)质点在A→B应作减速运动,当初动能最小时,到达B点的速度为零,根据能量守恒定律求出所需的最小初动能.
(2)质点在B→0的运动有三种可能情况,①质点在B→O作加速运动,对应条件为:mg≤
;②质点在B→O做减速运动,对应条件为:mg≥
,质点在B→O之间存在一个平衡点D,在B→D质点做减速运动,在D→O做加速运动,对应的条件为:
<mg<
,结合能量守恒定律求出不同条件下所需的最小初动能.
(2)质点在B→0的运动有三种可能情况,①质点在B→O作加速运动,对应条件为:mg≤
| 4kqQ |
| 9R2 |
| 4kqQ |
| R2 |
| 4kqQ |
| 9R2 |
| 4kqQ |
| R2 |
解答:解:(1)质点在A→B应作减速运动.设质点在A点的最小初动能为Ek0,则根据能量守恒得,可得质点刚好能达到B点的条件为:
-
+mgR=Ek0+
-
①
由此可得Ek0=mgR+
. ②
(2)质点在B→0的运动有三种可能情况:
①质点在B→O作加速运动(参看图1),对应条件为:
mg≤
③
此时只要质点能过B点,也必然能到达O点,因此质点能到达O点所需的最小动能由②式给出,即
Ek0=mgR+
. ④
若③式中取等号,则最小初动能比④式给出的Ek0略大一点.
②质点在B→O做减速运动(参看图1),对应条件为:
mg≥
⑤
此时质点刚好能到达O点的条件为:
-
+mg(2R)=Ek0+
-
⑥
由此可得Ek0=2mgR-
⑦
③质点在B→O之间存在一个平衡点D,(参看图2),在B→D质点做减速运动,在D→O做加速运动,对应的条件为:
<mg<
⑧
设D到O点的距离为x,则:
mg=
⑨
即x=
-
⑩
根据能量守恒,质点刚好能到达D点的条件为:
-
+mg(2R-x)=Ek0+
-
(11)
由⑩(11)两式可得质点到达D点的最小初动能为Ek0=
mgR+
-2
.
只要质点能通过D点也必然能到达O点,所以质点能到达O点的最小初动能也就是(12)式(严格讲应比(12)式给出的Ek0略大一点.)
答:(1)要使质点从 A 点上抛后能够到达B点,所需的最小初动能为Ek0=mgR+
.
(2)当mg≤
,最小初动能为Ek0=mgR+
;当mg≥
,最小初动能为Ek0=2mgR-
当
<mg<
,最小初动能为Ek0=
mgR+
-2
.
| kqQ |
| R |
| kqQ | ||
|
| kqQ |
| 2R |
| kqQ | ||
|
由此可得Ek0=mgR+
| 7kqQ |
| 30R |
(2)质点在B→0的运动有三种可能情况:
①质点在B→O作加速运动(参看图1),对应条件为:
mg≤
| 4kqQ |
| 9R2 |
此时只要质点能过B点,也必然能到达O点,因此质点能到达O点所需的最小动能由②式给出,即
Ek0=mgR+
| 7kqQ |
| 30R |
若③式中取等号,则最小初动能比④式给出的Ek0略大一点.
②质点在B→O做减速运动(参看图1),对应条件为:
mg≥
| 4kqQ |
| R2 |
此时质点刚好能到达O点的条件为:
| kqQ |
| R |
| kqQ | ||
|
| kqQ |
| 2R |
| kqQ | ||
|
由此可得Ek0=2mgR-
| 11kqQ |
| 10R |
③质点在B→O之间存在一个平衡点D,(参看图2),在B→D质点做减速运动,在D→O做加速运动,对应的条件为:
| 4kqQ |
| 9R2 |
| 4kqQ |
| R2 |
设D到O点的距离为x,则:
mg=
| kqQ | ||
(
|
即x=
|
| R |
| 2 |
根据能量守恒,质点刚好能到达D点的条件为:
| kqQ |
| R |
| kqQ | ||
(
|
| kqQ |
| 2R |
| kqQ | ||
|
由⑩(11)两式可得质点到达D点的最小初动能为Ek0=
| 5 |
| 2 |
| 9kqQ |
| 10R |
| kgmqQ |
只要质点能通过D点也必然能到达O点,所以质点能到达O点的最小初动能也就是(12)式(严格讲应比(12)式给出的Ek0略大一点.)
答:(1)要使质点从 A 点上抛后能够到达B点,所需的最小初动能为Ek0=mgR+
| 7kqQ |
| 30R |
(2)当mg≤
| 4kqQ |
| 9R2 |
| 7kqQ |
| 30R |
| 4kqQ |
| R2 |
| 11kqQ |
| 10R |
| 4kqQ |
| 9R2 |
| 4kqQ |
| R2 |
| 5 |
| 2 |
| 9kqQ |
| 10R |
| kgmqQ |

点评:解决本题的关键知道带电球面的电荷量可以等效到圆心,结合能量守恒定律进行求解,注意第二问中需分情况讨论.

练习册系列答案
相关题目
 如图所示,两个固定的等量异种电荷,在它们连线的垂直平分线上有a、b、c三点,则( )
如图所示,两个固定的等量异种电荷,在它们连线的垂直平分线上有a、b、c三点,则( )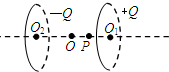 如图所示,两个固定的相同细环同轴放置,相距一定的距离,O1、O2分别为两环的圆心,O为O1、O2连线的中点,P在O的右侧.两环分别带有均匀分布的等量异种电荷.则( )
如图所示,两个固定的相同细环同轴放置,相距一定的距离,O1、O2分别为两环的圆心,O为O1、O2连线的中点,P在O的右侧.两环分别带有均匀分布的等量异种电荷.则( ) 如图所示,两个固定的相同细环相距一定的距离,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量电荷,一个重力不计的带正电的粒子从远处沿轴线飞来并穿过两环.则带电粒子运动过程中( )
如图所示,两个固定的相同细环相距一定的距离,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量电荷,一个重力不计的带正电的粒子从远处沿轴线飞来并穿过两环.则带电粒子运动过程中( )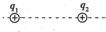 如图所示,两个固定的带正电的点电荷q1、q2,电荷量之比为1:4,相距为d,引入第三个点电荷q3,要使q3能处于平衡状态,对q3的位置、电性和电荷量的要求,以下叙述正确的是( )
如图所示,两个固定的带正电的点电荷q1、q2,电荷量之比为1:4,相距为d,引入第三个点电荷q3,要使q3能处于平衡状态,对q3的位置、电性和电荷量的要求,以下叙述正确的是( )