Question

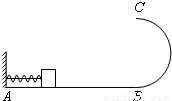
一段细绳把物体与墙面连接，物体与墙面之间有一个被压缩的弹簧，弹簧具有3.2J的弹性势能．已知水平段AB光滑，半圆段BC不光滑，其半径R=0.4m，物体质量m=0.1kg，g=10m/s²．若将细绳剪断，物体刚好可以到达最高点C．
（1）求物体离开弹簧后在水平段滑行的速度大小？
（2）求小球在C点的速度大小？
（3）求小球在BC段运动过程中摩擦做的功？

Answer 1

【答案】分析：清楚物体运动过程中能量的转化，根据能量守恒定律解决问题．
在C点进行受力分析，根据牛顿第二定律解决问题．
研究从B点到C点，运用动能定理求解功．
解答：解：（1）当物体脱离弹簧后，弹簧的弹性势能全部转化为物体的动能，
由能量守恒定律，得E_P=mv²  
求得：v=8 m/s                                                      
（2）物体刚好可以到达最高点C．
在C点，由牛顿第二定律得：mg=m
求得：v_c=2m/s
（3）从B点到C点，由动能定理得：
W_f-mgh=mv_c²-mv_B²
求得：W_f=-2.2J
（1）物体离开弹簧后在水平段滑行的速度大小是8 m/s 
（2）小球在C点的速度大小2m/s
（3）小球在BC段运动过程中摩擦做的功是-2.2J
点评：对于圆周运动的受力问题，我们要找出向心力的来源．
动能定理的应用范围很广，可以求速度、力、功等物理量，特别是可以去求变力功．