题目内容
如图甲所示，两平行金属板A、B的板长l=
m，板间距d= 0.10m，在金属板右侧有一范围足够大的方向垂直于纸面向里的匀强磁场，其边界为MN，与金属板垂直。在t=0时刻，两金属板间加如图乙所示的正弦交变电压，匀强磁场的磁感应强度B=1.0×10-2T。现从t=0开始，从两极板左侧的中点O以每秒钟1000个的数量不间断地释放出某种正电荷，这种带正电的粒子均以v0=
×105m/s的速度沿两板间的中线OO′连续进入电场，经电场后射入磁场。已知带电粒子的比荷
＝1.25×107C/kg，粒子的重力忽略不计，假设在粒子通过电场区域的极短时间内极板间的电压可以看作不变，不计粒子间的相互作用求：
⑴ t＝0时刻进入的粒子，经边界MN射入磁场和射出磁场时两点间的距离（结果保留两位有效数字）；
⑵每秒钟有多少个带正电的粒子进入磁场；
⑶何时由O点进入的带电粒子在磁场中运动的时间最长，最长时间为多少？（π≈3）
⑴t＝0时，UAB=0，带电粒子在极板间不偏转，水平射入磁场，
得 
① （2分）
射入和射出磁场时，两点间的距离为s＝2r ② （1分）
由①②可得s = 1.4m ③ （1分）
⑵设：当两极板电压为u时，由O点射入的粒子刚好从板的边缘进入磁场，则有
④（1分）
⑤（1分）
⑥（1分）
⑦（1分）
由④⑤⑥⑦式得： 
⑧（1分）
由乙图可知，在每周期内只有0～
，
～
，
～
，时间段内由O射入的粒子才能通过电场而进入磁场，即只有一半的时间内有粒子能进入磁场，所以每秒钟有500个粒子进入磁场（2分）
⑶只有当A板电势高于B板电势，且沿B板右侧边缘进入磁场的粒子，由于在电场中的偏转角最大，使得其在磁场中做圆周运动对应的圆心角最大，故在磁场中运动的时间最长，如图丙所示。即
,（
……）⑨（1分）
或
,（……）⑩（1分）
这些时刻入射的粒子在磁场中运动的时间最长。
由带电粒子在电场中做类平抛运动的特点可得
，θ=30° 11（2分）
设粒子在磁场中做匀速圆周运动的周期T，所求的最长时间为t′，则有
12（2分）
由几何关系得粒子在磁场中运动的圆心角240°，
则 
13（2分）
由12、13式代入数据得t′=3.2 ×s 14（1分）
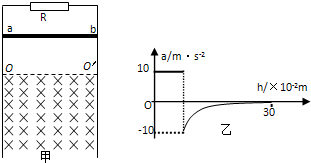（2011?徐州一模）如图甲所示，两条足够长的光滑平行金属导轨竖直放置，导轨问距为L=1m，两导轨的，上端间接有电阻，阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场，磁场磁感应强度为2T，现将质量m=0.1kg电阻不计的金届杆ab，从OO′上方某处由静止释放，金属杆在下落的过程中与导轨保持良好接触，且始终保持水平，不计导轨的电阻．已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示．求：
如图甲所示，两条足够长的光滑平行金属导轨竖直放置，导轨问距为L=1m，两导轨的，上端间接有电阻，阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场，磁场磁感应强度为2T，现将质量m=0.1kg电阻不计的金届杆ab，从OO′上方某处由静止释放，金属杆在下落的过程中与导轨保持良好接触，且始终保持水平，不计导轨的电阻．已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示．求：
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子．忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化．sin30=0.5，sin37=0.6，sin45=
．