题目内容
如图所示，一个质量为2kg的小球用一根长为1m的细绳连接，在竖直平面内做圆周运动．g=10m/s2．要使小球能顺利的通过最高点，则最高点的速度至少为| 10 |
| 10 |
30
30
N．分析：（1）小球恰好通过最高点时，细绳的拉力为零，由重力提供向心力，可由牛顿第二定律求出小球通过最高点时的速度；
（2）当它在最高点的速度大小为v=5m/s时，由绳子的拉力和重力的合力提供小球的向心力，根据牛顿第二定律求出绳子的拉力大小．
（2）当它在最高点的速度大小为v=5m/s时，由绳子的拉力和重力的合力提供小球的向心力，根据牛顿第二定律求出绳子的拉力大小．
解答：解：当小球恰好通过最高点时，细绳的拉力为零，由重力提供向心力，可由牛顿第二定律得
mg=m
解得，v0=
=
m/s
当它在最高点的速度大小为v=5m/s时，设绳子的拉力大小为F，则有
mg+F=m
代入解得 F=80N
故答案为：
，30
mg=m
| v02 |
| l |
解得，v0=
| gl |
| 10 |
当它在最高点的速度大小为v=5m/s时，设绳子的拉力大小为F，则有
mg+F=m
| v2 |
| l |
代入解得 F=80N
故答案为：
| 10 |
点评：本题中小球到达最高点的临界速度为v0=
，关键通过分析受力，确定向心力的来源．
| gl |
练习册系列答案
高中必刷题系列答案
相关题目
如图所示，一个质量为M的人站在台秤上，用跨过定滑轮的绳子，将质量为m的物体自高处放下，当物体以a加速下降（a＜g）时，台秤的读数为（ ）
如图所示．一个质量为m=10kg的物体，由1/4圆弧轨道上端从静止开始下滑，到达底端时的速度v=2.5m/s，然后沿水平面向右滑动1.0m的距离而停止．已知轨道半径R=0.4m，g=10m/s2，求：
如图所示，一个质量为m的小球用长为l的轻绳悬挂于O点，小球在水平拉恒力F的作用下，从平衡位置P点很缓慢地移动到Q点，则水平力F所做的功为（ ）
（2007?湖北模拟）如图所示，一个质量为m的小球被AO、BO两根细绳系住，BO绳为水平状态，AO绳与竖直方向的夹角为θ，此时AO绳对小球的拉力大小为T1．烧断BO绳后，小球摆动，当小球再次摆回到图中位置时AO绳对小球的拉力大小为T2．求：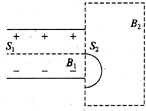
如图所示，一个质量为m，电荷量为q的带负电的粒子（重力不计），以初速度v由狭缝S1，垂直进入电场强度为E的匀强电场中．