题目内容
(2013?山西模拟)如图所示,一棱镜的截面为直角三角形ABC.∠A=60°.在此截面所在的平面内,一条光线从AB边上的M点.直射入棱镜,经AC边反射后从BC边射出,出射光线与BC边成45°.求:
(i)此棱镜的折射率;
(ii)将入射光线绕M点顺时针旋转θ角时,有光线AC边射出,则sinθ至少应大于多少?
(i)此棱镜的折射率;
(ii)将入射光线绕M点顺时针旋转θ角时,有光线AC边射出,则sinθ至少应大于多少?
分析:(i)由题意做出光路图,确定BC面的入射角和折射角,根据折射定律计算折射率.
(ii)将入射光线绕M点顺时针旋转θ角时,恰好光线在AC边不发生全反射是有光线AC边射出的临界情况.
(ii)将入射光线绕M点顺时针旋转θ角时,恰好光线在AC边不发生全反射是有光线AC边射出的临界情况.
解答:解:(i)棱镜内部的光线为MPN,设出射点N处光线的入射角为i,折射角为r,
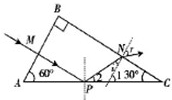
由反射定律及几何关系有:
i=∠1-∠2 ①
r=90°-45°=45° ②
由折射定律有:n=
③
解得:n=
④
(ii)将入射光线绕M点顺时针旋转θ角时,恰好光线在AC边发生全反射,设临界角为α,
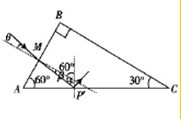
有:sinα=
⑤
此时M点的折射角为β,由几何关系有:
β=60°-α ⑥
由折射定律有:n=
⑦
解得:sinθ=
有光线从AC边射出时,sinθ至少应大于
.
答:(i)此棱镜的折射率为
;
(ii)将入射光线绕M点顺时针旋转θ角时,有光线AC边射出,则sinθ至少应大于
.

由反射定律及几何关系有:
i=∠1-∠2 ①
r=90°-45°=45° ②
由折射定律有:n=
| sini |
| sinr |
解得:n=
| 2 |
(ii)将入射光线绕M点顺时针旋转θ角时,恰好光线在AC边发生全反射,设临界角为α,

有:sinα=
| 1 |
| n |
此时M点的折射角为β,由几何关系有:
β=60°-α ⑥
由折射定律有:n=
| sinθ |
| sinβ |
解得:sinθ=
| ||
| 2 |
有光线从AC边射出时,sinθ至少应大于
| ||
| 2 |
答:(i)此棱镜的折射率为
| 2 |
(ii)将入射光线绕M点顺时针旋转θ角时,有光线AC边射出,则sinθ至少应大于
| ||
| 2 |
点评:本题根据反射定律和折射定律求解出各个分界面上的反射角和折射角,关键是画出光路图,并结合几何关系进行分析计算.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 (2013?山西模拟)如图所示,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O转动的轻杆,且摆到某处即能停在该处;另有一小钢球.现要利用这些器材测定弹簧被压缩时的弹性势能.
(2013?山西模拟)如图所示,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O转动的轻杆,且摆到某处即能停在该处;另有一小钢球.现要利用这些器材测定弹簧被压缩时的弹性势能.
 (2013?山西模拟)如图所示,A为静止于地球赤道上的物体,B为地球同步卫星,C为赤道平面内沿椭圆 轨道运行的卫星,P为B、C两卫星轨道的交点.下列说法中正确的是( )
(2013?山西模拟)如图所示,A为静止于地球赤道上的物体,B为地球同步卫星,C为赤道平面内沿椭圆 轨道运行的卫星,P为B、C两卫星轨道的交点.下列说法中正确的是( ) (2013?山西模拟)如图所示,一物块放在倾角为θ的传输带上,且物块始终与传输带相对静止.关于物块所受到的静摩擦力,下列说法正确的是( )
(2013?山西模拟)如图所示,一物块放在倾角为θ的传输带上,且物块始终与传输带相对静止.关于物块所受到的静摩擦力,下列说法正确的是( )