题目内容
如图所示,斜面的倾角为θ=37o,物块m1和m2之间用轻绳相连,m1=m2=1kg,斜面与m1之间的动摩擦因数为μ=0.25,m2离地面高度h=8m,系统由静止开始运动,假设斜面和轻绳足够长,求:(取g=10m/s2,sin37o=0.6,cos37°=0.8)
(1)m2在落地前瞬间速度多大?
(2)当m2落地后,m1还能向上滑行多远? 
(1)以m1、m2组成的系统为研究对象,由牛顿第二定律可得:
m2g―m1gsinθ―μm1gcosθ=(m1+m2)a 2分
则:a==1m/s2 2分
设m2落地时速度大小为v1,则:
v1===4m/s 2分
(2)m2落地后,m1沿斜面向上做匀减速运动,由牛顿第二定律可得:
m1gsinθ+μm1gcosθ=m1a' 2分
则: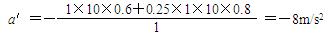 2分
2分
则m1还可滑行的距离为:
s===1m 2分
解析

练习册系列答案
相关题目
 如图所示,斜面的倾角θ=37°.一个质量m=1.0kg的物体,从静止开始沿斜面下滑.在开始运动后的最初2.0s内,物体下滑的距离为4.0m.不计空气阻力.计算时重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,斜面的倾角θ=37°.一个质量m=1.0kg的物体,从静止开始沿斜面下滑.在开始运动后的最初2.0s内,物体下滑的距离为4.0m.不计空气阻力.计算时重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,斜面的倾角为θ,圆柱体质量为m.若把重力沿垂直于墙面和垂直于斜面两个方向分解,则重力垂直于斜面的分力大小为
如图所示,斜面的倾角为θ,圆柱体质量为m.若把重力沿垂直于墙面和垂直于斜面两个方向分解,则重力垂直于斜面的分力大小为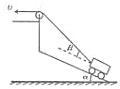 如图所示,斜面的倾角为α,人用跨过定滑轮的绳子拉小车.现人以速度v匀速拉动绳子,当拉小车的绳子与斜面的夹角为β时,小车沿斜面运动的速度为( )
如图所示,斜面的倾角为α,人用跨过定滑轮的绳子拉小车.现人以速度v匀速拉动绳子,当拉小车的绳子与斜面的夹角为β时,小车沿斜面运动的速度为( )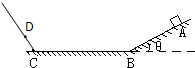 如图所示,斜面的倾角θ=37°,一物块从斜面A点由静止释放.物块质量m=10kg,物块与水平面的动摩擦因数μ=0.4,其余部分光滑,不计物块滑至B、C点时由于碰撞的能量损失,最后能够上升到D点.已知AB高度差H=1.8m,CD高度差为h=0.6m,(取g=10m/s2,sin37°=0.6,cos37°=0.8)( )
如图所示,斜面的倾角θ=37°,一物块从斜面A点由静止释放.物块质量m=10kg,物块与水平面的动摩擦因数μ=0.4,其余部分光滑,不计物块滑至B、C点时由于碰撞的能量损失,最后能够上升到D点.已知AB高度差H=1.8m,CD高度差为h=0.6m,(取g=10m/s2,sin37°=0.6,cos37°=0.8)( )