题目内容
如图甲所示,两平行金属板间存在相互垂直的电场和磁场,两金属板间的电压为U,板间距离为d,两板间的磁场在3t0内的变化规律如图乙所示.左侧的粒子源沿中心线OO’以v0的速度不断发射质量为m、电荷量为+q的粒子(不计重力).已知t=0时刻进入两板间的带电粒子,恰好沿中心线运动,并在t0时刻从O’点穿出两板.
(1)求磁感应强度B0的方向和大小;
(2)若
t0时刻进入两板间的粒子也能从板间飞出,求飞出时偏离O’点的距离.

(1)求磁感应强度B0的方向和大小;
(2)若
| 1 |
| 2 |

(1)带电粒子受的电场力竖直向下,则洛伦兹力的方向竖直向上,由左手定则可判断出磁感应强度的方向垂直纸面向里.
带电粒子沿中心线做匀速直线运动,有:qv0B0=q
则磁感应强度的大小为:B0=
.
(2)从
t0时刻进入两板间的带电粒子,在
t0时间内做匀速直线运动,然后在电场力的作用下做类平抛运动.
粒子做类平抛运动的时间为t=
t0
竖直方向有:y=
at2
由牛顿第二定律得:a=
解得:y=
.
答:(1)磁感应强度B0的方向垂直纸面向里,大小为
.
(2)飞出时偏离O’点的距离为
.
带电粒子沿中心线做匀速直线运动,有:qv0B0=q
| U |
| d |
则磁感应强度的大小为:B0=
| U |
| dv0 |
(2)从
| 1 |
| 2 |
| 1 |
| 2 |
粒子做类平抛运动的时间为t=
| 1 |
| 2 |
竖直方向有:y=
| 1 |
| 2 |
由牛顿第二定律得:a=
| qU |
| md |
解得:y=
| qUt02 |
| 8md |
答:(1)磁感应强度B0的方向垂直纸面向里,大小为
| U |
| dv0 |
(2)飞出时偏离O’点的距离为
| qUt02 |
| 8md |

练习册系列答案
相关题目
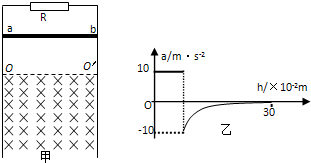 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:

 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: =1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45=
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45= .
.