Question

（9分）如图所示，一质量为M的平板车B放在光滑水平面上，在其右端放一质量为m的小木块A，m＜M，A、B间动摩擦因数为μ，现给A和B以大小相等、方向相反的初速度v₀，使A开始向左运动，B开始向右运动，最后A不会滑离B，求：

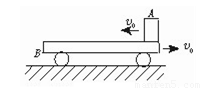
（1）A、B最后的速度大小和方向.

（2）从地面上看，小木块向左运动到离出发点最远处时，平板车向右运动的位移大小.

 

Answer 1

【答案】

（1）v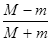＝ v₀，方向向右    （2）s=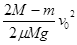

【解析】

试题分析：（1）A刚好没有滑离B板，表示当A滑到B板的最左端时，A、B具有相同的速度，设此速度为v，A和B的初速度的大小为v₀，则据动量守恒定律可得：Mv₀－mv₀=（M+m）v   2分

解得：v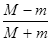＝ v₀，方向向右         1分

（2）从地面上看，小木块向左运动到离出发点最远处时，木块速度为零，平板车速度为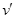，由动量守恒定律得  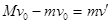               2分

这一过程平板向右运动S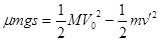，      2分

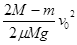解得s=       2分

考点：本题考查动量守恒和能量守恒定律的应用。