题目内容
质量为M的木块静止在光滑的水平面上,质量为m的子弹以水平速度v在下面两种情况下击中木块,并最终留在木块内.第一次木块被事先固定住,子弹在木块中钻入深度为s1,经历时间为t1;第二次木块不固定,子弹在木块中钻入深度为s2,经历时间为t2.两次击中木块过程中,子弹受的平均阻力相同.比较s1和s2,t1和t2,有( )A.s1=s2
B.s1<s2
C.t1<t2
D.t1>t2
【答案】分析:根据能量守恒定律研究系统摩擦生热Q=fs,其中f为阻力,s为子弹相对于木块的位移.
两次击中木块过程中,子弹受的平均阻力相同,两次子弹的动量变化不等,根据动量定理研究子弹比较时间.
解答:解:A、第一次木块被事先固定住,子弹在木块中钻入深度为s1,
根据能量守恒定律可知,系统摩擦生热Q1= mv2.
mv2.
第二次木块不固定,子弹在木块中钻入深度为s2,
根据能量守恒定律可知,系统摩擦生热Q2= mv2-
mv2- (M+m)v2,
(M+m)v2,
所以Q1>Q2.
根据能量守恒定律可知,系统摩擦生热Q=fs.其中f为阻力,s为子弹相对于木块的位移.
所以s1>s2.故A、B错误.
C、两次击中木块过程中,子弹受的平均阻力相同,两次子弹的动量变化不等,根据动量定理研究子弹得:
第一次木块被事先固定住,
ft1=mv-0
第二次木块不固定,
ft2=mv-mv
所以t1>t2.故C错误,D正确.
故选D.
点评:本题考查了动量定理和能量守恒定律在子弹打木块模型中的应用,注意研究对象的选取和功能关系的应用.
两次击中木块过程中,子弹受的平均阻力相同,两次子弹的动量变化不等,根据动量定理研究子弹比较时间.
解答:解:A、第一次木块被事先固定住,子弹在木块中钻入深度为s1,
根据能量守恒定律可知,系统摩擦生热Q1=
 mv2.
mv2.第二次木块不固定,子弹在木块中钻入深度为s2,
根据能量守恒定律可知,系统摩擦生热Q2=
 mv2-
mv2- (M+m)v2,
(M+m)v2,所以Q1>Q2.
根据能量守恒定律可知,系统摩擦生热Q=fs.其中f为阻力,s为子弹相对于木块的位移.
所以s1>s2.故A、B错误.
C、两次击中木块过程中,子弹受的平均阻力相同,两次子弹的动量变化不等,根据动量定理研究子弹得:
第一次木块被事先固定住,
ft1=mv-0
第二次木块不固定,
ft2=mv-mv
所以t1>t2.故C错误,D正确.
故选D.
点评:本题考查了动量定理和能量守恒定律在子弹打木块模型中的应用,注意研究对象的选取和功能关系的应用.

练习册系列答案
相关题目
如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为s1,木块发生的位移为s2,子弹进入木块深度为s,子弹受到阻力大小恒为f,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列说法中不正确的是( )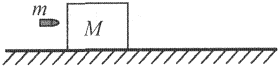

A、fs1=
| ||||||
B、fs2=
| ||||||
C、fs=
| ||||||
D、fs=
|
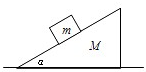 倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )
倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )| A、木块受到的摩擦力大小是mgcosα | B、木块对斜两体的压力大小是mgsinα | C、桌面对斜面体的摩擦力大小是mgsinαcosα | D、桌面对斜面体的支持力大小是(M+m)g |
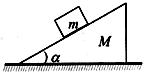 倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )
倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )| A、木块受到的摩擦力大小是mgsinα | B、木块对斜面体的压力大小是mgcosα | C、桌面对斜面体的摩擦力大小是mgsinαcosα | D、桌面对斜面体的支持力大小是(M+m)g |
