Question

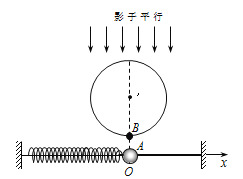
【题目】如图所示，质量相等的物块A和足够长的木板B，质量为m1=m2=1kg，通过一劲度系数k=25N/m的轻质弹簧连接。B与水平面间接触面的动摩擦因数μ=0.25，A、B间接触面光滑，弹簧开始时处于原长。现在物块A上施加一个水平向右的恒力F=5N，使物块A向右滑动，物块运动过程中弹簧始终处在弹性限度内。已知最大静摩擦力与滑动摩擦力大小相等，重力加速度g取10m/s2，弹簧弹性势能可表示为 ,其中k为弹簧劲度系数，x为弹簧形变量。求：

（1）物块A刚开始滑动时加速度大小a；

（2）木板B刚开始滑动时弹簧的伸长量x0和物块A的速度大小v0；

（3）弹簧第一次拉伸到最长时弹簧的伸长量x.

Answer 1

【答案】(1) (2) (3)

【解析】（1）对物块A受力分析有：

（2）对物块B受力分析，①，且②，

联立①②解得③；

对物块A应用功能关系有：④

联立③④解得⑤；

（3）设从物块B开始运动到弹簧第一次最长A位移为，物块B位移为，弹簧伸长量为x，弹簧最长时A、B速度相等，为v，则对A、B系统应用功能关系可得：⑥；

对A、B组成的系统，受到恒力F和地面摩擦力的作用，合力为零，A、B系统动量守恒⑦；由长度关系⑧；

联立解得（舍去）和；

故弹簧第一次拉伸最长时弹簧伸长量为；