题目内容
 在如图所示的电路中,合上电键S,变阻器的滑动头C从A端滑至B端的过程中,电路中的一些物理量的变化关系如甲、乙、丙三图所示.电表、导线对电路的影响不计.(甲图为电源的效率η与外电路电阻R的关系曲线,这里的效率指电源的输出功率与总功率的比值;乙图为输出功率P与路端电压U的关系曲线;丙图为路端电压U与总电流I的关系曲线.)
在如图所示的电路中,合上电键S,变阻器的滑动头C从A端滑至B端的过程中,电路中的一些物理量的变化关系如甲、乙、丙三图所示.电表、导线对电路的影响不计.(甲图为电源的效率η与外电路电阻R的关系曲线,这里的效率指电源的输出功率与总功率的比值;乙图为输出功率P与路端电压U的关系曲线;丙图为路端电压U与总电流I的关系曲线.)(1)请根据图甲求出滑动变阻器最大阻值Rm与电源内阻r之比;
(2)电路中电源电动势E、内阻r不变,请写出在滑动变阻器滑动头C从A端滑至B端的过程中电源输出功率P与路端电压U的函数关系式(用字母表示);
(3)分别写出甲、乙、丙三图中的a、b、c、d各点的坐标(求出数值并注明单位).

分析:(1)当外电阻最大时,电源的效率最高,由最大效率求出变阻器最大阻值Rm与电源内阻r之比
(2)根据功率公式、欧姆定律求解
(3)根据功率公式、欧姆定律分别求出各点的坐标.
(2)根据功率公式、欧姆定律求解
(3)根据功率公式、欧姆定律分别求出各点的坐标.
解答:解:(1)η=
=
,
当外电阻最大时,电源的效率最高,
=80%
可解得
=4:1
(2)根据功率公式得
P=UI=U
=
(3)由P=
可知当U=
时P有最大值
,
又由乙图可知
=4.5W
由丙图可知当U=0时,I=
=
=3A
由上两式可求出E=6V,r=2Ω
进一步可求出Rm=8Ω
当滑片移到B端时,U=
E=4.8V,P=
=2.88W,I=
=0.6A
所以有:a(8Ω,80%),b(3V,4.5W),c(4.8V,2.88W),d(0.6A,4.8V)
答:(1)滑动变阻器最大阻值Rm与电源内阻r之比
=4:1;
(2)在滑动变阻器滑动头C从A端滑至B端的过程中电源输出功率P与路端电压U的函数关系式P=
(3)甲、乙、丙三图中的a、b、c、d各点的坐标分别是a(8Ω,80%),b(3V,4.5W),c(4.8V,2.88W),d(0.6A,4.8V)
| I2R |
| I2(R+r) |
| R |
| (R+r) |
当外电阻最大时,电源的效率最高,
| Rm |
| (Rm+r) |
可解得
| Rm |
| r |
(2)根据功率公式得
P=UI=U
| E-U |
| r |
| EU-U2 |
| r |
(3)由P=
| EU-U2 |
| r |
| E |
| 2 |
| E2 |
| 4r |
又由乙图可知
| E2 |
| 4r |
由丙图可知当U=0时,I=
| E-U |
| r |
| E |
| r |
由上两式可求出E=6V,r=2Ω
进一步可求出Rm=8Ω
当滑片移到B端时,U=
| 4 |
| 5 |
| U2 |
| Rm |
| U |
| Rm |
所以有:a(8Ω,80%),b(3V,4.5W),c(4.8V,2.88W),d(0.6A,4.8V)
答:(1)滑动变阻器最大阻值Rm与电源内阻r之比
| Rm |
| r |
(2)在滑动变阻器滑动头C从A端滑至B端的过程中电源输出功率P与路端电压U的函数关系式P=
| EU-U2 |
| r |
(3)甲、乙、丙三图中的a、b、c、d各点的坐标分别是a(8Ω,80%),b(3V,4.5W),c(4.8V,2.88W),d(0.6A,4.8V)
点评:本题要理解电源的输出功率、路端电压和效率与外电阻的关系,要注意三个图象对应的关系,比较复杂.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 标有“8V 6.4W”和“8V 20W”字样的L1、L2两只灯泡连接在如图所示的电路中,C点接地.如果将电路中L1、L2两灯的位置互换,则( )
标有“8V 6.4W”和“8V 20W”字样的L1、L2两只灯泡连接在如图所示的电路中,C点接地.如果将电路中L1、L2两灯的位置互换,则( ) (2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
(2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( ) 在如图所示的电路中,R3=4Ω,A的示数为0.75A,V的示数为2V.突然有一个电阻被烧断,使得A的示数变为0.80A,V的示数变为3.2V(图中电表均视为理想电表).?
在如图所示的电路中,R3=4Ω,A的示数为0.75A,V的示数为2V.突然有一个电阻被烧断,使得A的示数变为0.80A,V的示数变为3.2V(图中电表均视为理想电表).? (2012?西城区模拟)在如图所示的电路中,电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=4.0Ω,不计电流表的内阻.闭合开关S后,电流表的示数为( )
(2012?西城区模拟)在如图所示的电路中,电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=4.0Ω,不计电流表的内阻.闭合开关S后,电流表的示数为( )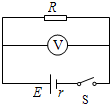 在如图所示的电路中,已知电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=2.0Ω.闭合开关S后,电阻R两端的电压U等于( )
在如图所示的电路中,已知电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=2.0Ω.闭合开关S后,电阻R两端的电压U等于( )