题目内容
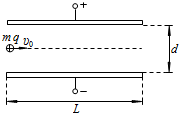 如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.
如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.(1)求离子在穿过两板的过程中沿垂直金属板方向上移动的距离y;
(2)若在两板间加垂直纸面的匀强磁场,发现离子束恰好沿直线穿过两板,求磁场磁感应
强度B的大小和方向;
(3)若增大两板间匀强磁场的强度,发现离子束在穿过两板的过程中沿垂直金属板方向上移动的距离也为y,求离子穿出两板时速度的大小υ.
分析:(1)粒子穿过电场时,粒子做类平抛运动,由水平方向上的直线运动和竖直方向上的匀加速直线运动规律可得出离子移动的距离;
(2)加入磁场后,粒子沿直线运动,则可知洛仑兹力与电场力平衡,由左手定则可得出磁场的方向,由平衡关系可得出磁感应强度的大小;
(3)已知粒子偏转位移,则由动能定理可求得离子穿出两板时速度的大小.
(2)加入磁场后,粒子沿直线运动,则可知洛仑兹力与电场力平衡,由左手定则可得出磁场的方向,由平衡关系可得出磁感应强度的大小;
(3)已知粒子偏转位移,则由动能定理可求得离子穿出两板时速度的大小.
解答:解:(1)离子在穿过两板的过程中,只受与初速度v0垂直的电场力F作用,离子的加速度
a=
=
离子沿中心轴线方向做匀速直线运动,设离子穿过两板经历的时间为t,则L=v0t
离子沿垂直金属板方向上做初速度为0的匀变速直线运动,则y=
at2
解得
离子移动的距离为 y=
(2)离子束恰好沿直线穿过两板,说明离子受力平衡,即 qE=qv0B
所以磁感应强度的大小 B=
磁场的方向垂直纸面向里.
(3)增大磁场的强度时,离子受洛伦兹力增大,所以离子会向上偏.在离子穿过极板的过程中,电场力做负功,根据动能定理得 -qEy=
mv2-
m
解得离子穿出两板时的速度:v=
=
.
a=
| F |
| m |
| qU |
| md |
离子沿中心轴线方向做匀速直线运动,设离子穿过两板经历的时间为t,则L=v0t
离子沿垂直金属板方向上做初速度为0的匀变速直线运动,则y=
| 1 |
| 2 |
解得
离子移动的距离为 y=
| qUL2 | ||
2md
|
(2)离子束恰好沿直线穿过两板,说明离子受力平衡,即 qE=qv0B
所以磁感应强度的大小 B=
| U |
| dv0 |
磁场的方向垂直纸面向里.
(3)增大磁场的强度时,离子受洛伦兹力增大,所以离子会向上偏.在离子穿过极板的过程中,电场力做负功,根据动能定理得 -qEy=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得离子穿出两板时的速度:v=
|
|
点评:带电粒子在电磁场中的运动一般有直线运动、圆周运动和一般的曲线运动;直线运动一般由动力学公式求解,圆周运动由洛仑兹力充当向心力,一般的曲线运动一般由动能定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
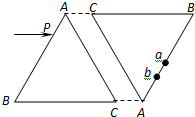 如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后从a、b两点射出.对于从a、b射出的这两束光下列说法中正确的( )
如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后从a、b两点射出.对于从a、b射出的这两束光下列说法中正确的( )| A、在玻璃中,从a点射出光的传播速度比从b点射出光的传播速度大 | B、从a点射出的为蓝光,从b点射出的为红光 | C、从a、b两点射出的两束光仍平行,且平行于BC | D、从a、b两点射出的两束光不平行 |
 (2010?江西模拟)如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中.两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后变为从a、b两点射出的单色光.对于这两束单色光,下列判断正确的是( )
(2010?江西模拟)如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中.两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后变为从a、b两点射出的单色光.对于这两束单色光,下列判断正确的是( ) (2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求:
(2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求: 如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.且L>d,上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.
如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.且L>d,上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.