题目内容
如图所示,两根不可伸长的细绳,一端分别系在竖直杆上A、B两点上,另一端共同系拴住一小球C.当杆以ω转动时,两绳恰好都拉直,此后ω逐渐增大,则两绳张力变化情况是( )
A.AC张力增大,BC张力不变
B.AC张力不变,BC张力增大
C.AC张力减小,BC张力增大
D.AC张力增大,BC张力减小
【答案】分析:小球做圆周运动,竖直方向上的合力为零,水平方向上合力提供向心力,根据牛顿第二定律判断两根绳子的拉力的变化.
解答:解:在竖直方向上,有:TAcosθ=mg
水平方向上有: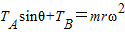
知θ角不变,则AC绳张力不变,角速度增大,则BC绳张力增大.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键知道小球做圆周运动向心力的来源,抓住AC绳与竖直方向的夹角不变,结合牛顿第二定律进行求解.
解答:解:在竖直方向上,有:TAcosθ=mg
水平方向上有:
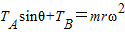
知θ角不变,则AC绳张力不变,角速度增大,则BC绳张力增大.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键知道小球做圆周运动向心力的来源,抓住AC绳与竖直方向的夹角不变,结合牛顿第二定律进行求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
