题目内容
如图所示，在竖直放置的圆柱形容器内用质量为m的活塞密封一部分气体，活塞与容器壁间能无摩擦滑动，容器的横截面积为S，将整个装置放在大气压恒为p的空气中，开始时气体的温度为T，活塞与容器底的距离为h，当气体从外界吸收热量Q后，活塞缓慢上升d后再次平衡，问：①外界空气的温度是多少？
②在此过程中的密闭气体的内能增加了多少？
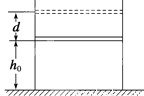
【答案】分析：由盖-吕萨克定律求温度，由热力学第一定律得△U=W+Q=Q-pSh-mgh，其中pSh为克服大气压力做的功．
解答：解：（1）取密闭气体为研究对象，活塞上升过程为等压变化，由盖-吕萨克定律有
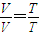
得外界温度T=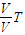
=
=
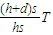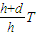
（2）活塞上升的过程，密闭气体克服大气压力和活塞的重力做功，所以外界对系统做的功W=-（mg+PS）d
根据热力学第一定律得密闭气体增加的内能△U=Q+W=Q-（mg+PS）d
答：①外界空气的温度是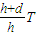
②在此过程中的密闭气体的内能增加了Q-（mg+PS）d
点评：本题考查了理想气体状态方程和热力学第一定律的应用，难度中等．
解答：解：（1）取密闭气体为研究对象，活塞上升过程为等压变化，由盖-吕萨克定律有
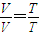
得外界温度T=
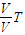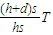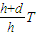
==（2）活塞上升的过程，密闭气体克服大气压力和活塞的重力做功，所以外界对系统做的功W=-（mg+PS）d
根据热力学第一定律得密闭气体增加的内能△U=Q+W=Q-（mg+PS）d
答：①外界空气的温度是
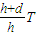
②在此过程中的密闭气体的内能增加了Q-（mg+PS）d
点评：本题考查了理想气体状态方程和热力学第一定律的应用，难度中等．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
如图所示，在竖直放置的光滑半圆弧绝缘细管的圆心O处固定一点电荷，将质量为m，带电量为+q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力．求：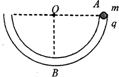
如图所示，在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷，将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无作用力．若小球所带电荷量很小，不影响O点处的点电荷的电场，则放于圆心O处的点电荷在OB连线的中点处的电场强度大小（ ）
如图所示，在竖直放置的半圆形容器的中心O点分别以水平速度v1，v2抛出两个小球（可视为质点），最终它们分别落在圆弧上的A点和B点，已知OA与OB相互垂直且OA与竖直方向成a角，求两小球初速度之比v1，：v2．
如图所示，在竖直放置的光滑绝缘的半圆形细管的圆心O处放一点电荷，将质量为m、带电量为q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力，则放于圆心处的电荷在AB弧中点处的电场强度大小为（ ）
（2012?东城区三模）如图所示，在竖直放置的金属板M上放一个放射源C，可向纸面内各个方向射出速率均为v的α粒子，P是与金属板M平行的足够大的荧光屏，到M的距离为d．现在P与金属板M间加上垂直纸面的匀强磁场，调整磁感应强度的大小，恰使沿M板向上射出的α粒子刚好垂直打在荧光屏上．若α粒子的质量为m，电荷量为+2e．则（ ）