题目内容
如图所示,半径为r=0.10m的圆形匀强磁场区域边界跟x轴相切于坐标原点O,磁感应强度按图示规律变化,方向垂直直纸面向里,在t=0时刻由O处沿y轴正方向射入速度为v=1.0×103m/s的带负电粒子,已知粒子质量m=9.0×10-12kg,电量q=9.0×10-6C,不计粒子重力,求粒子在磁场中的运动时间和离开磁场时的位置坐标.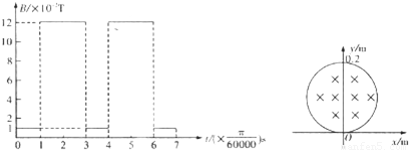
【答案】分析:粒子进入磁场后,由洛伦兹力提供向心力,做匀速圆周运动,设单位时间t=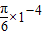 s,根据牛顿第二定律求出粒子的轨迹半径和周期T,根据t与T的关系,分析在第一个单位时间内粒子在磁场中转过的圆心角.在第二单位时间内,用同样的方法求出粒子在磁场中转过的圆心角,画出轨迹,确定经过几个单位时间,粒子刚好射出磁场,即可求得时间和离开磁场时的位置坐标.
s,根据牛顿第二定律求出粒子的轨迹半径和周期T,根据t与T的关系,分析在第一个单位时间内粒子在磁场中转过的圆心角.在第二单位时间内,用同样的方法求出粒子在磁场中转过的圆心角,画出轨迹,确定经过几个单位时间,粒子刚好射出磁场,即可求得时间和离开磁场时的位置坐标.
解答:解:粒子进入磁场后,由洛伦兹力提供向心力,做匀速圆周运动,设单位时间t=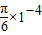 s.则
s.则
在第一个t内,B1=1×10-2T
由qvB1=m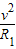
得,R1=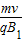 =0.1m
=0.1m
T1=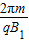 =2π×10-4s
=2π×10-4s
故t=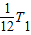
则粒子在第一个t内,在磁场中转过的圆心角为30°.
在第二个t内,B2=12×10-2T
T2=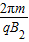 =
=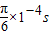
则t=T2,
故粒子在第二个和第三t内刚好做两个完整的圆周运动,第四个t内的运动与第一t内的相同,第五、六个t内的运动又与第二、第三个t内的相同,到第七个t末,粒子刚好出磁场,
由上分析可知,粒子在磁场中运动时间为
t′=7t=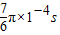 ,运动轨迹如图,离开磁场时的位置坐标为(0.1,0.1)
,运动轨迹如图,离开磁场时的位置坐标为(0.1,0.1)
答:粒子在磁场中的运动时间是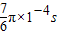 ,离开磁场时的位置坐标为(0.1,0.1).
,离开磁场时的位置坐标为(0.1,0.1).
点评:本题关键是采用归纳法,总结出粒子在每个t时间内转过的圆心角,画出轨迹进行求解.
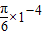 s,根据牛顿第二定律求出粒子的轨迹半径和周期T,根据t与T的关系,分析在第一个单位时间内粒子在磁场中转过的圆心角.在第二单位时间内,用同样的方法求出粒子在磁场中转过的圆心角,画出轨迹,确定经过几个单位时间,粒子刚好射出磁场,即可求得时间和离开磁场时的位置坐标.
s,根据牛顿第二定律求出粒子的轨迹半径和周期T,根据t与T的关系,分析在第一个单位时间内粒子在磁场中转过的圆心角.在第二单位时间内,用同样的方法求出粒子在磁场中转过的圆心角,画出轨迹,确定经过几个单位时间,粒子刚好射出磁场,即可求得时间和离开磁场时的位置坐标.解答:解:粒子进入磁场后,由洛伦兹力提供向心力,做匀速圆周运动,设单位时间t=
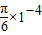 s.则
s.则在第一个t内,B1=1×10-2T
由qvB1=m
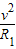
得,R1=
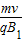 =0.1m
=0.1mT1=
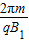 =2π×10-4s
=2π×10-4s故t=
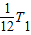
则粒子在第一个t内,在磁场中转过的圆心角为30°.
在第二个t内,B2=12×10-2T
T2=
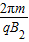 =
=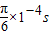
则t=T2,
故粒子在第二个和第三t内刚好做两个完整的圆周运动,第四个t内的运动与第一t内的相同,第五、六个t内的运动又与第二、第三个t内的相同,到第七个t末,粒子刚好出磁场,
由上分析可知,粒子在磁场中运动时间为
t′=7t=
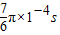 ,运动轨迹如图,离开磁场时的位置坐标为(0.1,0.1)
,运动轨迹如图,离开磁场时的位置坐标为(0.1,0.1)答:粒子在磁场中的运动时间是
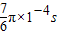 ,离开磁场时的位置坐标为(0.1,0.1).
,离开磁场时的位置坐标为(0.1,0.1).点评:本题关键是采用归纳法,总结出粒子在每个t时间内转过的圆心角,画出轨迹进行求解.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 (2006?淮北模拟)如图所示,半径为R,内径很小的光滑半圆管竖直放置.两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离.
(2006?淮北模拟)如图所示,半径为R,内径很小的光滑半圆管竖直放置.两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离. 如图所示,半径为R 的光滑圆形轨道竖直固定放置,质量为m 的小球在圆形轨道内侧做圆周运动.小球通过轨道最高点时恰好与轨道间没有相互作用力.已知当地的重力加速度大小为g,不计空气阻力.试求:
如图所示,半径为R 的光滑圆形轨道竖直固定放置,质量为m 的小球在圆形轨道内侧做圆周运动.小球通过轨道最高点时恰好与轨道间没有相互作用力.已知当地的重力加速度大小为g,不计空气阻力.试求: 如图所示,半径为R的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ(认为最大静摩擦力等于滑动摩擦力),现要使A不下落,则圆筒转动的角速度ω至少为( )
如图所示,半径为R的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ(认为最大静摩擦力等于滑动摩擦力),现要使A不下落,则圆筒转动的角速度ω至少为( )
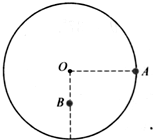 如图所示,半径为R,质量不计的圆盘盘面与地面相垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘处固定一个质量为m的小球A,在O点的正下方离O点R/2处固定一个质量也为m的小球B,放开盘让其自由转动,问:
如图所示,半径为R,质量不计的圆盘盘面与地面相垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘处固定一个质量为m的小球A,在O点的正下方离O点R/2处固定一个质量也为m的小球B,放开盘让其自由转动,问: