题目内容
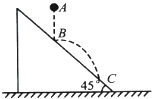
【题目】如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞.已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力.求:
(1)小球在AB段运动过程中重力做功的平均功率P;
(2)小球落到C点时速度的大小.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据匀变速直线运动的速度位移公式求出小球到达B点的速度,再根据平均速度公式求出这段位移内的平均速度,从而求出重力做功的平均功率.
(2)从B点反弹后做平抛运动,根据平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,求出运动的时间,求出竖直分速度,根据平行四边形定则求出合速度,即C点的速度.
解:(1)小球下降过程中,做自由落体运动,落到斜面B点的速度为v,
满足:2gh=v2
解得:![]()
所以小球在AB段重力的平均功率:![]()
(2)小球从B到C做平抛运动,设B到C的时间为t,
竖直方向:![]()
水平方向:xBCcosθ=vt
解得:t=![]()
所以C点的速度为![]() .
.

练习册系列答案
相关题目