题目内容
如图所示，在水平转台的光滑水平横杆上穿有两个质量分别为2m和m的小球A和B，A、B间用劲度系数为k的轻质弹簧连接，弹簧的自然长度为L，当转台以角速度ω绕坚直轴匀速转动时，如果A、B仍能相对横杆静止而不碰左右两壁，求：
（1）A、B两球分别离开中心转轴的距离；
（2）若转台的直径为2L，求角速度ω的取值范围．
（1）A、B两球分别离开中心转轴的距离；
（2）若转台的直径为2L，求角速度ω的取值范围．
（1）因为弹簧对A、B两球的弹力相等，知A、B两球做圆周运动的向心力相等，有：
2mrAω2=mrBω2
所以：rB=2rA．
根据牛顿第二定律得：2mrAω2=k(rA+rB-L)
解得：rA=
，rB=
．
（2）若转台的直径为2L，则rB＜L．
因为：rB=
，解得：ω＜
．
答：（1）A、B两球分别离开中心转轴的距离分别为：rA=
，rB=
．
（2）角速度ω的取值范围为ω＜
．
2mrAω2=mrBω2
所以：rB=2rA．
根据牛顿第二定律得：2mrAω2=k(rA+rB-L)
解得：rA=
| kL |
| 3k-2mω2 |
| 2kL |
| 3k-2mω2 |
（2）若转台的直径为2L，则rB＜L．
因为：rB=
| 2kL |
| 3k-2mω2 |
|
答：（1）A、B两球分别离开中心转轴的距离分别为：rA=
| kL |
| 3k-2mω2 |
| 2kL |
| 3k-2mω2 |
（2）角速度ω的取值范围为ω＜
|
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
如图所示，在水平转台的光滑水平横杆上穿有两个质量分别为2m和m的小球A和B，A、B间用劲度系数为k的轻质弹簧连接，弹簧的自然长度为L，当转台以角速度ω绕竖直轴匀速转动时，如果A、B仍能相对横杆静止而不碰左右两壁，求：
如图所示叠放在水平转台上的小物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为3m、2m、m，A与B、B与转台、C与转台间的动摩擦因数都为μ，B、C离转台中心的距离分别为r、1.5r．设本题中的最大静摩擦力等于滑动摩擦力．以下说法中不正确的是（ ）
如图所示，在水平转台上放一个质量M=2kg的木块，它与转台间最大静摩擦力fmax=6.0N，绳的一端系住木块，穿过转台的中心孔O（孔光滑），另一端悬挂一个质量m=1.0kg的小物块，当转台以ω=5rad/s匀速转动时，木块相对转台静止，则木块到O点的距离可以是（M、m均视为质点，g取10m/s2）（ ）
如图所示，在水平转台上放置有轻绳相连的质量相同的滑块1和滑块2，转台绕转轴OO′以角速度ω匀运转动过程中，轻绳始终处于水平状态，两滑块始终相对转台静止，且与转台之间的动摩擦因数相同，滑块1到转轴的距离小于滑块2到转轴的距离．关于滑块1和滑块2受到的摩擦力f1和f2与ω2的关系图线，可能正确的是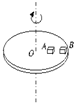
如图所示，在水平转台上放有A、B两个小物块，它们到轴心O的距离分别为rA=0.2m，rB=0.5m，它们与台面间静摩擦力的最大值为其重力的0.4倍，取g=10m/s2．