题目内容
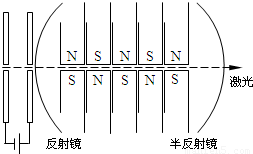 自由电子激光器原理如图所示,自由电子经电场加速后,从正中央射入上下排列着许多磁铁的磁场区域,相邻两磁铁相互紧靠且极性相反.电子在磁场力作用下“扭动”着前进,每“扭动”一次就会发出一个光子(不计电子发出光子后能量损失),两端的反射镜使光子来回反射,最后从透光的一端发射出激光.
自由电子激光器原理如图所示,自由电子经电场加速后,从正中央射入上下排列着许多磁铁的磁场区域,相邻两磁铁相互紧靠且极性相反.电子在磁场力作用下“扭动”着前进,每“扭动”一次就会发出一个光子(不计电子发出光子后能量损失),两端的反射镜使光子来回反射,最后从透光的一端发射出激光.(1)若激光器发射激光的功率为P=6.63×109W,频率为f=1016Hz,试求该激光器每秒发出的光子数(普朗克常量h=6.63×10-34J.s);
(2)若加速电压U=1.8×104V,电子质量m=9.0×10-31kg,电子电量e=1.6×10-19c,每对磁极间的磁场可看作是匀强磁场,磁感应强度B=9.0×10-4T,每个磁极左右宽L1=0.30m,垂直纸面方向长L2=1.Om.当电子从正中央垂直磁场方向射入时,电子可通过几对磁极?
【答案】分析:(1)求出每个光子所带能量,根据激光器的发射功率可以求出激光光子数;
(2)由几何关系,求出侧移量,从而确定通过磁极的个数;
解答:解:(1)每个激光光子的能量:E=hυ ①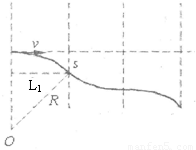
设激光器每秒发射n个光子 P=nE ②
由①②联立解得:n=1.0×1027 ③
(2)设电子经电场加速获得的速度为v,
由动能定理有:eU= mv2 ④
mv2 ④
设电子在磁场中做圆周运动的轨道半径为R,
evB=m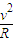 ⑤
⑤
电子穿过每对磁极的侧移距离均相同,设每次侧移为s,如图所示,
由图可知s=R-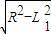 ⑥
⑥
电子通过的磁极个数:N=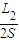
解得:N=5
答:
(1)该激光器每秒发出的光子数为1.0×1027.
(2)当电子从正中央垂直磁场方向射入时,电子可通过5对磁极.
点评:本题考查电子在电场中加速,在磁场中偏转,并由动能定理、牛顿第二定律及几何关系来综合解题,从而培养学生形成一定的套路.
(2)由几何关系,求出侧移量,从而确定通过磁极的个数;
解答:解:(1)每个激光光子的能量:E=hυ ①

设激光器每秒发射n个光子 P=nE ②
由①②联立解得:n=1.0×1027 ③
(2)设电子经电场加速获得的速度为v,
由动能定理有:eU=
 mv2 ④
mv2 ④设电子在磁场中做圆周运动的轨道半径为R,
evB=m
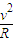 ⑤
⑤电子穿过每对磁极的侧移距离均相同,设每次侧移为s,如图所示,
由图可知s=R-
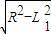 ⑥
⑥电子通过的磁极个数:N=
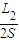
解得:N=5
答:
(1)该激光器每秒发出的光子数为1.0×1027.
(2)当电子从正中央垂直磁场方向射入时,电子可通过5对磁极.
点评:本题考查电子在电场中加速,在磁场中偏转,并由动能定理、牛顿第二定律及几何关系来综合解题,从而培养学生形成一定的套路.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 自由电子激光器原理如图所示,自由电子经电场加速后,从正中央射入上下排列着许多磁铁的磁场区域,相邻两磁铁相互紧靠且极性相反.电子在磁场力作用下“扭动”着前进,每“扭动”一次就会发出一个光子(不计电子发出光子后能量损失),两端的反射镜使光子来回反射,最后从透光的一端发射出激光.
自由电子激光器原理如图所示,自由电子经电场加速后,从正中央射入上下排列着许多磁铁的磁场区域,相邻两磁铁相互紧靠且极性相反.电子在磁场力作用下“扭动”着前进,每“扭动”一次就会发出一个光子(不计电子发出光子后能量损失),两端的反射镜使光子来回反射,最后从透光的一端发射出激光.
