题目内容
如图所示，水平绳与轻弹簧共同固定一个重球静止，弹簧与竖直方向成θ角．现剪断水平绳，在绳断时，重球的加速度大小为gtanθ
gtanθ
，方向水平向左
水平向左
．分析：对小球受力分析，由共点力的平衡条件可求得绳子拉力的大小；由于弹簧的弹力不能突变，则弹簧的弹力与重力的合力等于绳子的拉力，再由牛顿第二定律可求得加速度．
解答：解：对小球受力分析，小球受重力、弹力及绳子的拉力而处于平衡状态；则由共点力的平衡条件可知，绳子的拉力F=mgtanθ；
因弹簧的弹力不能突变，重力不变，故二力的合力仍等于绳子的拉力，故合外力F合=mgtanθ；
由牛顿第二定律可知，加速度a=gtanθ；方向水平向左；
故答案为：gtanθ；水平向左．
因弹簧的弹力不能突变，重力不变，故二力的合力仍等于绳子的拉力，故合外力F合=mgtanθ；
由牛顿第二定律可知，加速度a=gtanθ；方向水平向左；
故答案为：gtanθ；水平向左．
点评：本题要注意明确弹簧的弹力不能突变，同时根据共点力的平衡条件可知，弹簧的弹力与重力的合力与绳子的拉力大小相等，方向相反．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
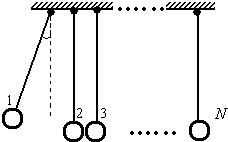某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔，从左到右，球的编号依次为1、2、3…N，球的质量依次递减，每球质量与其相邻左球质量之比为k（k＜1）．将1号球向左拉起，然后由静止释放，使其与2号球碰撞，2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰．（不计空气阻力，忽略绳的伸长，g取10m/s2）
如图所示，细绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2，线框A1的电阻R，质量为M，物块A2的质量为m（M＞m），两匀强磁场区域Ⅰ、Ⅱ的高度也为L，磁感应强度均为B，方向水平且与线框平面垂直．线框ab边距磁场边界
如图所示，水平绳与轻弹簧共同固定一个重球静止，弹簧与竖直方向成θ角．现剪断水平绳，在绳断时，重球的加速度大小为________，方向________．
。如在A端挂上G=20N的重物，求细绳所受的拉力和轻杆受到的压力。