题目内容
13. 单匝矩形线圈abcd绕ad边为轴在匀强磁场B中匀速转动,如图所示,图中ab=L1,bc=L2,线框电阻为r,ad间接入的电阻为R.R与理想电流表A串联,线圈角速度为ω,求:
单匝矩形线圈abcd绕ad边为轴在匀强磁场B中匀速转动,如图所示,图中ab=L1,bc=L2,线框电阻为r,ad间接入的电阻为R.R与理想电流表A串联,线圈角速度为ω,求:(1)电流表A的读数和图示位置时bc边受到的安培力;
(2)从图示位置转过90°的过程中通过电流表的总电量q.
(3)从图示位置转过90°的过程中电阻R上产生的热量Q热.
分析 (1)根据电动势最大值Em=BSω求出最大值,然后有欧姆定律求电流最大值,根据I=$\frac{{I}_{m}}{\sqrt{2}}$知电表读数,根据F=BIL求安培力.
(2)根据q=$\frac{△∅}{R+r}$求解电荷量;
(3)根据Q=I2Rt求解电热Q.
解答 解:(1)电动势最大值Em=BSω=BL1L2ω
电流最大值${I_m}=\frac{E_m}{R+r}=\frac{{B{L_1}L{\;}_2ω}}{R+r}$
电流表示数为有效值${I_A}=\frac{I_m}{{\sqrt{2}}}=\frac{{B{L_1}{L_2}ω}}{{\sqrt{2}(R+r)}}$
bc所受安培力大小$F=BI{L_2}=\frac{{{B^2}{L_1}L_2^2ω}}{R+r}$
(2)从图示位置转过90°的过程中通过电流表的总电量$q=\overline I•△t=\frac{△ϕ}{R+r}=\frac{{B{L_1}{L_2}}}{R+r}$
(3)从图示位置转过90°的过程中电阻R上产生的热量$Q={I^2}•R•t=\frac{{{B^2}L_1^2L_2^2ω}}{{2{{(R+r)}^2}}}•R•\frac{π}{2ω}=\frac{{πωR{B^2}L_1^2L_2^2}}{{4{{(R+r)}^2}}}$
答:(1)电流表A的读数为$\frac{B{L}_{1}{{L}^{\;}}_{2}ω}{\sqrt{2}(R+r)}$,图示位置时bc边受到的安培力为$\frac{{B}^{2}{L}_{1}{{L}_{2}^{2}ω}_{\;}}{R+r}$;
(2)从图示位置转过90°的过程中通过电流表的总电量q为$\frac{B{L}_{1}{L}_{2}}{R+r}$.
(3)从图示位置转过90°的过程中电阻R上产生的热量Q热为$\frac{πωR{B}^{2}{L}_{1}^{2}{L}_{2}^{2}}{4(R+r)^{2}}$.
点评 此题考查交流电的描述,知道电表读数、功率、能量用到交流电的有效值,求解电荷量要用到交流电的平均值.

| A. | 光敏电阻 | B. | 热敏电阻 | C. | 霍尔元件 | D. | 声音传感器 |
 如图所示,电路中完全相同的三只灯泡L1、L2、L3分别与电阻R、电感L、电容C串联,然后再并联到220V、50Hz的交流电路上,三只灯泡亮度恰好相同.若保持交变电压有效值不变,而将频率提高到100Hz,则发生的现象是( )
如图所示,电路中完全相同的三只灯泡L1、L2、L3分别与电阻R、电感L、电容C串联,然后再并联到220V、50Hz的交流电路上,三只灯泡亮度恰好相同.若保持交变电压有效值不变,而将频率提高到100Hz,则发生的现象是( )| A. | 三灯亮度不变 | B. | 三灯均变亮 | ||
| C. | L1亮度不变、L2变亮、L3变暗 | D. | L1亮度不变、L2变暗、L3变亮 |
| A. | 匀速圆周运动速度不断改变 | B. | 匀速圆周运动加速度不变 | ||
| C. | 匀速圆周运动是一种变加速运动 | D. | 匀速圆周运动的物体处于平衡状态 |
| A. | 开普勒认为所有的行星运动轨道为同一个椭圆,太阳位于这个椭圆的焦点上 | |
| B. | 行星沿椭圆轨道运行时,在近日点线速度大,在远日点线速度小 | |
| C. | 各行星绕太阳沿椭圆运行的半长轴与周期的比值都相等 | |
| D. | 各行星的运动轨道离太阳有近有远,离太阳距离远的行星运动周期小 |
 如图所示,在玻璃管的水中有一红蜡块正在匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的( )
如图所示,在玻璃管的水中有一红蜡块正在匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的( )| A. | 直线P | B. | 曲线Q | ||
| C. | 曲线R | D. | 无法确定是P还是Q |
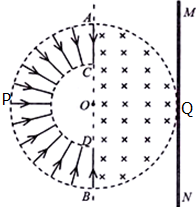 “太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行边界ACDB,O到MN板的距离OQ为L.在边界ACDB和收集板MN之间有一以O为圆心,L为半径的半圆形匀强磁场,磁场方向垂直纸面向内.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子引力的影响.
“太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行边界ACDB,O到MN板的距离OQ为L.在边界ACDB和收集板MN之间有一以O为圆心,L为半径的半圆形匀强磁场,磁场方向垂直纸面向内.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子引力的影响.