题目内容
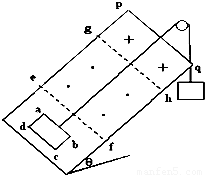
光滑斜面倾角θ=30°,在斜面上放置一矩形线框abcd,ab边长L1=1m,bc边长L2=0.6m,线框质量m=1kg电阻R=0.1Ω.线框用细线通过定滑轮与重物相连,重物质量M=2kg.斜面上ef线与gh线(ef∥gh∥pq)间有垂直斜面向上的匀强磁场,磁感应强度B1=0.5T.gh线与pq线间有垂直斜面向下的匀强磁场,磁感应强度B2=0.5T.如果线框从静止开始运动,当ab边进入磁场时恰好做匀速直线运动,ab边由静止开始运动到gh线所用时间2.3s.问:(ⅰ)ef线和gh线间距?
(ⅱ)ab边由静止开始运动到gh线这段时间内产生的焦耳热?
(ⅲ)ab边刚进入gh线瞬间线框的加速度?
【答案】分析:(1)ab边进入磁场时做匀速运动,根据平衡条件和安培力表达式F=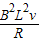 ,求出ab的速度,根据牛顿第二定律求出abcd进磁场B1前做匀加速直线运动的加速度,再由运动学公式可求出线框从静止到进入磁场B1前和进入磁场B1过程的时间,由总时间得到完全进入磁场后的时间,由运动学即可求出ef线和gh线间距.
,求出ab的速度,根据牛顿第二定律求出abcd进磁场B1前做匀加速直线运动的加速度,再由运动学公式可求出线框从静止到进入磁场B1前和进入磁场B1过程的时间,由总时间得到完全进入磁场后的时间,由运动学即可求出ef线和gh线间距.
(2)ab边由静止开始运动到gh线这段时间内产生焦耳热Q等于线框克服安培力做功.
(3)ab边刚进入gh线瞬间,线框中ab和dc两边都切割磁感线,各产生一个感应电动势,根据牛顿第二定律求解加速度.
解答: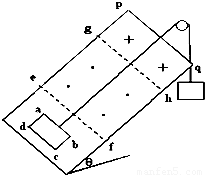 解:(ⅰ)ab边进入磁场时做匀速运动,受力平衡,则有:
解:(ⅰ)ab边进入磁场时做匀速运动,受力平衡,则有:
T=mgsinθ+FA
又E=BL1v1、I=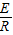 、FA=B1IL1,
、FA=B1IL1,
对M:T=Mg
联立解得,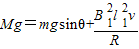
代入解得 v=6m/s
abcd进磁场B1前做匀加速直线运动
对整体:Mg-mgsinθ=(M+m)a
联立得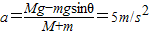
则该阶段运动的时间 t1=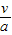 =1.2s
=1.2s
线框进入磁场B1过程做匀速运动的时间 t2=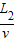 =0.1s
=0.1s
完全进入磁场后的加速度a=5m/s2,此阶段时间t3=t-t1-t2=1s
ef线和gh线间距s=L2+v1t3+ at32=9.1m
at32=9.1m
此时线框速度v2=v1+at3=11m/s
(ⅱ)ab边由静止开始运动到gh线这段时间内产生焦耳热Q=FAL2=(Mg-mgsinθ)l2=9J
(ⅲ)ab边刚进入gh线瞬间线框的加速度沿斜面向下.
由mgsinθ+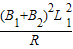 v2-Mg=(M+m)a2
v2-Mg=(M+m)a2
得a2=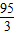 m/s2
m/s2
答:
(ⅰ)ef线和gh线间距是9.1m.
(ⅱ)ab边由静止开始运动到gh线这段时间内产生的焦耳热是9J.
(ⅲ)ab边刚进入gh线瞬间线框的加速度是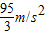 .
.
点评:本题过程较多,但物理情景比较简单,是电磁感应与力学基本知识的综合,只要熟练掌握基础知识,就能正确求解.
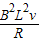 ,求出ab的速度,根据牛顿第二定律求出abcd进磁场B1前做匀加速直线运动的加速度,再由运动学公式可求出线框从静止到进入磁场B1前和进入磁场B1过程的时间,由总时间得到完全进入磁场后的时间,由运动学即可求出ef线和gh线间距.
,求出ab的速度,根据牛顿第二定律求出abcd进磁场B1前做匀加速直线运动的加速度,再由运动学公式可求出线框从静止到进入磁场B1前和进入磁场B1过程的时间,由总时间得到完全进入磁场后的时间,由运动学即可求出ef线和gh线间距.(2)ab边由静止开始运动到gh线这段时间内产生焦耳热Q等于线框克服安培力做功.
(3)ab边刚进入gh线瞬间,线框中ab和dc两边都切割磁感线,各产生一个感应电动势,根据牛顿第二定律求解加速度.
解答:
 解:(ⅰ)ab边进入磁场时做匀速运动,受力平衡,则有:
解:(ⅰ)ab边进入磁场时做匀速运动,受力平衡,则有:T=mgsinθ+FA
又E=BL1v1、I=
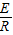 、FA=B1IL1,
、FA=B1IL1,对M:T=Mg
联立解得,
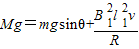
代入解得 v=6m/s
abcd进磁场B1前做匀加速直线运动
对整体:Mg-mgsinθ=(M+m)a
联立得
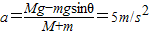
则该阶段运动的时间 t1=
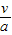 =1.2s
=1.2s线框进入磁场B1过程做匀速运动的时间 t2=
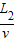 =0.1s
=0.1s完全进入磁场后的加速度a=5m/s2,此阶段时间t3=t-t1-t2=1s
ef线和gh线间距s=L2+v1t3+
 at32=9.1m
at32=9.1m此时线框速度v2=v1+at3=11m/s
(ⅱ)ab边由静止开始运动到gh线这段时间内产生焦耳热Q=FAL2=(Mg-mgsinθ)l2=9J
(ⅲ)ab边刚进入gh线瞬间线框的加速度沿斜面向下.
由mgsinθ+
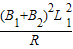 v2-Mg=(M+m)a2
v2-Mg=(M+m)a2得a2=
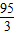 m/s2
m/s2答:
(ⅰ)ef线和gh线间距是9.1m.
(ⅱ)ab边由静止开始运动到gh线这段时间内产生的焦耳热是9J.
(ⅲ)ab边刚进入gh线瞬间线框的加速度是
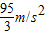 .
.点评:本题过程较多,但物理情景比较简单,是电磁感应与力学基本知识的综合,只要熟练掌握基础知识,就能正确求解.

练习册系列答案
相关题目
 如图所示,光滑斜面倾角θ=30°,一小球从距斜面底端O点正上方高度h=5m处由静止下落,小滑块从斜面上的P点由静止沿斜面下滑,若小球和滑块同时开始运动并在O点相遇,不计空气阻力,g取10m/s2.求OP之间的距离L.
如图所示,光滑斜面倾角θ=30°,一小球从距斜面底端O点正上方高度h=5m处由静止下落,小滑块从斜面上的P点由静止沿斜面下滑,若小球和滑块同时开始运动并在O点相遇,不计空气阻力,g取10m/s2.求OP之间的距离L. 光滑斜面倾角θ=30°,在斜面上放置一矩形线框abcd,ab边长L1=1m,bc边长L2=0.6m,线框质量m=1kg电阻R=0.1Ω.线框用细线通过定滑轮与重物相连,重物质量M=2kg.斜面上ef线与gh线(ef∥gh∥pq)间有垂直斜面向上的匀强磁场,磁感应强度B1=0.5T.gh线与pq线间有垂直斜面向下的匀强磁场,磁感应强度B2=0.5T.如果线框从静止开始运动,当ab边进入磁场时恰好做匀速直线运动,ab边由静止开始运动到gh线所用时间2.3s.
光滑斜面倾角θ=30°,在斜面上放置一矩形线框abcd,ab边长L1=1m,bc边长L2=0.6m,线框质量m=1kg电阻R=0.1Ω.线框用细线通过定滑轮与重物相连,重物质量M=2kg.斜面上ef线与gh线(ef∥gh∥pq)间有垂直斜面向上的匀强磁场,磁感应强度B1=0.5T.gh线与pq线间有垂直斜面向下的匀强磁场,磁感应强度B2=0.5T.如果线框从静止开始运动,当ab边进入磁场时恰好做匀速直线运动,ab边由静止开始运动到gh线所用时间2.3s. 如图所示,足够长的光滑斜面倾角θ=30°,一个带正电、电量为q的物体停在斜面底端B.现在加上一个沿斜面向上的场强为E的匀强电场,在物体运动到A点时撤销电场,那么:
如图所示,足够长的光滑斜面倾角θ=30°,一个带正电、电量为q的物体停在斜面底端B.现在加上一个沿斜面向上的场强为E的匀强电场,在物体运动到A点时撤销电场,那么:
