题目内容
13.如图所示,光滑水平地面上有一质量为2m,长为L=1.6m的木板,质量为m可视为质点的物块以v0=3m/s的水平初速度冲上木板,距木板前方s=0.6m处有倾角为θ=37°的固定斜面,物块与木板达到共速后木板与斜面碰撞并粘连,斜面足够长且左端和木板B端等高,已知物块与木板间动摩擦因数μ1=0.2,物块与斜面间动摩擦因数μ2=0.5(sin37°=0.6,cos37°=0.8,g=10m/s2)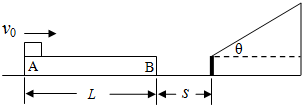
(1)求物块冲上木板后物块和木板的加速度;
(2)求碰撞前物块和木板达到的共同速度v;
(3)不计物体经过木板与斜面交界时的能量损失,求物块最终停下的位置.
分析 (1)根据牛顿第二定律分别求得加速度;
(2)根据速度时间公式求得共同速度;
(3)根据牛顿第二定律分别求得上滑和下滑过程中的加速度,利用运动学公式求得最终在木板上的位置
解答 解:(1)对物块:有牛顿第二定律可知:μ1mg=ma1
代入数据得:${a}_{1}=2m/{s}^{2}$,方向水平向左
对木板:有牛顿第二定律可知:μ1mg=2ma2
代入数据得:${a}_{2}=1m/{s}^{2}$,方向水平向右
(2)设t秒后达到共同速度
对物块:v=v0-a1t
对木板:v2=a2t
解得:v=1m/s,t=1s
(3)在t时间内,
物块位移:${x}_{1}={v}_{0}t-\frac{1}{2}{a}_{1}{t}^{2}$
木板位移:${x}_{2}=\frac{1}{2}{a}_{2}{t}^{2}$
相对位移:△x=x1-x2
联立解得:△x=1.5m
碰撞后木板粘连,物块减速,设冲上斜面时的速度为v2,有:${v}^{2}{-v}_{2}^{2}=2{a}_{1}{x}_{3}$
此时物块距木板B端:x3=L-△x=0.1m
滑上斜面过程:mgsinθ+μ2mgcosθ=ma3
${v}_{2}^{2}=2{a}_{3}{x}_{4}$
因为mgsinθ>μ2mgcosθ,物体不能停在斜面上
滑下斜面过程:mgsinθ-μ2mgcosθ=ma4,${v}_{3}^{2}=2{a}_{4}{x}_{4}$
回到小车上后匀减速到停下:${v}_{3}^{2}=2{a}_{1}{x}_{5}$
由以上各式解得:x5=0.03m,
故物块最终停下的位置距木板B端0.03m
答:(1)物块冲上木板后物块2m/s2和木板的加速度为1m/s2;
(2)求碰撞前物块和木板达到的共同速度v为1m/s;
(3)不计物体经过木板与斜面交界时的能量损失,物块最终停下的位置距木板B端0.03m
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,注意有摩擦时,上滑和下滑的加速度大小不等.

| A. | 路程为50m | |
| B. | 位移大小为40m,方向向上 | |
| C. | 速度改变量的大小为20m/s,方向向下 | |
| D. | 平均速度大小为10m/s,方向向上 |
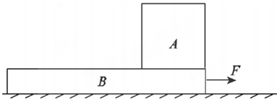 如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{μ}{2}$,最大静摩擦力等于滑动摩擦力,重力加速度为g,现对B施加一水平拉力F,则( )
如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{μ}{2}$,最大静摩擦力等于滑动摩擦力,重力加速度为g,现对B施加一水平拉力F,则( )| A. | 当F<3μmg时,A、B都相对地面静止 | |
| B. | 当F=$\frac{5}{2}$μmg时,A的加速度为$\frac{μg}{3}$ | |
| C. | 当F>6μmg时,A相对B滑动 | |
| D. | 无论F为何值,A的加速度不会超过μg |
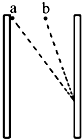 如图所示,竖直放置的两平行金属板间有匀强电场,在两极板间同一等高线上有两质量相等的带电小球a、b(可以看作质点).将小球a、b分别从紧靠左极板和两极板正中央的位置由静止释放,它们沿图中虚线运动,都能打在右极板上的同一点.则从释放小球到刚要打到右极板的运动中,下列说法正确的是( )
如图所示,竖直放置的两平行金属板间有匀强电场,在两极板间同一等高线上有两质量相等的带电小球a、b(可以看作质点).将小球a、b分别从紧靠左极板和两极板正中央的位置由静止释放,它们沿图中虚线运动,都能打在右极板上的同一点.则从释放小球到刚要打到右极板的运动中,下列说法正确的是( )| A. | 它们的运动时间ta>tb | |
| B. | 它们的电荷量之比qa:qb=2:1 | |
| C. | 它们的电势能减少量之比△Epa:△Epb=4:1 | |
| D. | 它们的动能增加量之比△Eka:△Ekb=4:1 |
| A. | 功是能量转化的量度 | |
| B. | 若某一个力对物体不做功,说明该物体一定没有位移 | |
| C. | 因为功有正负,所以其加减适用于平行四边形定则或三角形法则 | |
| D. | 一个恒力对物体做的功等于这个力的大小、物体位移的大小及力和位移夹角的余弦三者的乘积 |
| A. | 物体M的加速度比P的加速度大 | |
| B. | 物体P的加速度变化比M的速度变化快 | |
| C. | 物体P的速度可能在增加 | |
| D. | 物体M的速度一定在增加 |
 空间存在沿水平方向,电场强度大小为E的足够大的匀强电场,用绝缘细线系一个质量为m的带电小球,线的另一端固定于O点,平衡时悬线与竖直方向成α角,如图所示,则:
空间存在沿水平方向,电场强度大小为E的足够大的匀强电场,用绝缘细线系一个质量为m的带电小球,线的另一端固定于O点,平衡时悬线与竖直方向成α角,如图所示,则: 如图所示,物体的质量m=4kg,与水平地面间的动摩擦因数为μ=0.2,在倾角为37°,F=10N的恒力作用下,由静止开始做加速运动,当t=5s时撤去F,求(g=10m/s2)
如图所示,物体的质量m=4kg,与水平地面间的动摩擦因数为μ=0.2,在倾角为37°,F=10N的恒力作用下,由静止开始做加速运动,当t=5s时撤去F,求(g=10m/s2)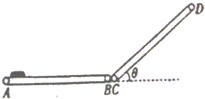 如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).
如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).