题目内容
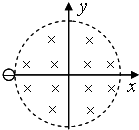如图所示，有一半径为R、有明显边界的圆形匀强磁场区域，磁感应强度为B．今有一电子沿x轴正方向射入磁场，恰好沿y轴负方向射出．如果电子的荷质比为| e | m |
（1）电子射入磁场时的速度；
（2）电子在磁场中运动的时间．
分析：带电粒子在洛伦兹力作用下，在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律可求得出轨道半径．根据粒子在磁场中偏转的角度与时间的关系求得粒子在磁场中运动的时间．
解答：解：（1）如图做出粒子运动的轨迹，由几何关系可知电子轨迹半径为R，
由洛伦兹力提供向心力有：evB=
解得：v=
（2）粒子的周期：T=
=
粒子运动的轨迹为
圆弧，所以：t=
T=
答：（1）电子射入磁场时的速度v=
；
（2）电子在磁场中运动的时间t=
．
由洛伦兹力提供向心力有：evB=
| mv2 |
| R |
解得：v=
| eBR |
| m |
（2）粒子的周期：T=
| 2πR |
| v |
| 2πm |
| qB |
粒子运动的轨迹为
| 1 |
| 4 |
| 1 |
| 4 |
| πm |
| 2eB |
答：（1）电子射入磁场时的速度v=
| eBR |
| m |
（2）电子在磁场中运动的时间t=
| πm |
| 2eB |
点评：该题考查到了带电粒子在匀强磁场中做圆周运动的半径的推导，洛伦兹力提供向心力；带电粒子在圆形区域的匀强磁场中的偏转角，与在磁场中的弧长是成正比的，弧长越长，所对应的弦长也就越长，要会熟练的利用几何关系求解圆心角．
练习册系列答案
相关题目
如图所示，有一半径为R质量为m的半球形凹槽P，放在光滑的水平地面上，一面紧靠在光滑的墙壁上，在槽口正上方某处有一质量为m的小球，由静止释放，落下后可沿光滑的球面滑下．试问：
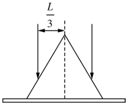（2012?湖南模拟）桌面上有一玻璃圆锥，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，此三角形的边长为L，如图所示，有一半径为
如图所示，有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中，磁场方向垂直纸面向里且与圆环平面垂直，圆环的电阻为R．若磁感应强度B在时间△t内均匀减小至零，则此过程（ ）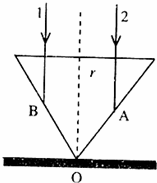
在桌面上有一个倒立的透明的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为n=1.73．r为已知，求：