题目内容
中国计划在2017年实现返回式月球软着陆器对月球进行科学探测，宇航员在月球上着陆后，自高h处以初速度v水平抛出一小球，测出水平射程为L（这时月球表面可以看作是平坦的），已知月球半径为R，万有引力常量为G，求：（1）月球表面处的重力加速度及月球的质量M月？
（2）如果要在月球上发射一颗绕月球运行的卫星，所需的最小发射速度为多大？
（3）当着陆器绕距月球表面高H的轨道上运动时，着陆器环绕月球运动的周期是多少？
【答案】分析：（1）平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据平抛运动的知识求出月球表面的重力加速度．根据万有引力等于重力求出月球的质量．
（2）以最小速度发射的卫星将贴着月球的表面运行，轨道半径等于月球的半径．根据万有引力提供向心力求出最小的发射速度．
（3）根据万有引力提供向心力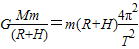
求着陆器环绕月球运动的周期．
解答：解：（1）由平抛运动得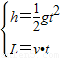
∴
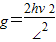
着陆器在月球表面有：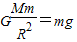
∴
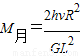
故月球表面处的重力加速度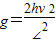
，月球的质量
．
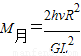（2）着陆器绕月球表面运行有：
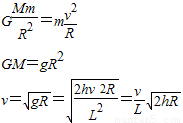
故最小的发射速度为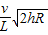
．
（3）由牛顿第二定律有：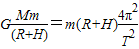
而GM=gR2
∴
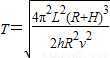
故着陆器环绕月球运动的周期为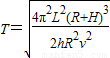
．
点评：解决本题的关键掌握万有引力等于重力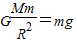
，以及万有引力提供做卫星做圆周运动的向心力．
（2）以最小速度发射的卫星将贴着月球的表面运行，轨道半径等于月球的半径．根据万有引力提供向心力求出最小的发射速度．
（3）根据万有引力提供向心力
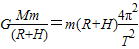求着陆器环绕月球运动的周期．解答：解：（1）由平抛运动得
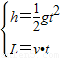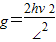
∴着陆器在月球表面有：
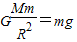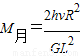
∴故月球表面处的重力加速度
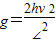，月球的质量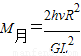．（2）着陆器绕月球表面运行有：
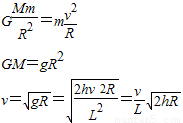
故最小的发射速度为
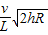．（3）由牛顿第二定律有：
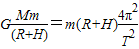
而GM=gR2
∴
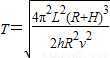
故着陆器环绕月球运动的周期为
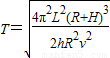．点评：解决本题的关键掌握万有引力等于重力
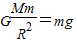，以及万有引力提供做卫星做圆周运动的向心力． 
练习册系列答案
相关题目
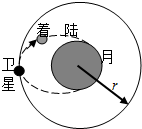中国计划在2017年实现返回式月球软着陆器对月球进行科学探测，如图所示．届时发射一颗运动半径为r的绕月卫星，登月着陆器从绕月卫星出发，沿椭圆轨道降落到月球的表面上，与月球表面经多次碰撞和弹跳才停下来．假设着陆器第一次弹起的最大高度为h，水平速度为v1，第二次着陆时速度为v2．已知月球半径为R，着陆器质量为m，不计一切阻力和月球的自转．求：
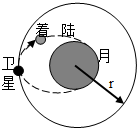中国计划在2017年实现返回式月球软着陆器对月球进行科学探测，如图所示，届时发射一颗运动半径为r的绕月卫星，登月着陆器从绕月卫星出发，沿椭圆轨道降落到月球的表面上，与月球表面经多次碰撞和弹跳才停下来，假设着陆器第一次弹起的最大高度为h，水平速度为v1，第二次着陆时速度为v2，已知月球半径为R，着陆器质量为m，不计一切阻力和月球的自转．求：