题目内容
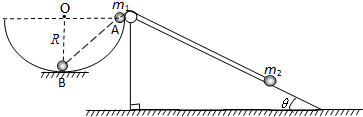
如图所示,左侧为一个半径为R的半球形的碗固定在水平桌面上,碗口水平,O点为球心,碗的内表面及碗口光滑.右侧是一个固定光滑斜面,斜面足够长,倾角θ=30°.一根不可伸长的不计质量的细绳跨在碗口及光滑斜面顶端的光滑定滑轮两端上,线的两端分别系有可视为质点的小球m1和m2,且m1>m2.开始时m1恰在右端碗口水平直径A处,m2在斜面上且距离斜面顶端足够远,此时连接两球的细绳与斜面平行且恰好伸直.当m1由静止释放运动到圆心O的正下方B点时细绳突然断开,不计细绳断开瞬间的能量损失.
(1)求小球m2沿斜面上升的最大距离s;
(2)若已知细绳断开后小球m1沿碗的内侧上升的最大高度为R/2,求
= .

(1)求小球m2沿斜面上升的最大距离s;
(2)若已知细绳断开后小球m1沿碗的内侧上升的最大高度为R/2,求
| m1 | m2 |
分析:(1)先根据运动合成与分解求出小球m1到达最低点B时m1、m2速度关系,对m1、m2系统由功能关系列出方程,细绳断后m2沿斜面上升,对m2由机械能守恒定律列出方程,根据几何关系写出小球m2沿斜面上升的最大距离的表达式,联立方程即可求解;
(2)对 m1由机械能守恒定律列出方程,结合(1)中的方程,联立即可求解.
(2)对 m1由机械能守恒定律列出方程,结合(1)中的方程,联立即可求解.
解答:解:(1)设重力加速度为g,小球m1到达最低点B时m1、m2速度大小分别为v1、v2,
由运动合成与分解得v1=
v2①
对m1、m2系统由功能关系得
m1gR-m2gh=
m1v12+
m2v22②
h=
Rsin30°③
设细绳断后m2沿斜面上升的距离为s′,对m2由机械能守恒定律得m2gs′sin30°=
m2v
④
小球m2沿斜面上升的最大距离s=
R+s′⑤
联立得s=(
+
)R⑥
(2)对 m1由机械能守恒定律得:
m1v12=m1g
⑦
联立①②③⑦得
=
≈1.9
答:(1)求小球m2沿斜面上升的最大距离为(
+
)R;(2)1.9
由运动合成与分解得v1=
| 2 |
对m1、m2系统由功能关系得
m1gR-m2gh=
| 1 |
| 2 |
| 1 |
| 2 |
h=
| 2 |
设细绳断后m2沿斜面上升的距离为s′,对m2由机械能守恒定律得m2gs′sin30°=
| 1 |
| 2 |
2 2 |
小球m2沿斜面上升的最大距离s=
| 2 |
联立得s=(
| 2 |
2m1-
| ||
| 2m1+m2 |
(2)对 m1由机械能守恒定律得:
| 1 |
| 2 |
| R |
| 2 |
联立①②③⑦得
| m1 |
| m2 |
2
| ||
| 2 |
答:(1)求小球m2沿斜面上升的最大距离为(
| 2 |
2m1-
| ||
| 2m1+m2 |
点评:本题主要考查了机械能守恒定律,运动合成分解知识,学生综合分析理解及运算能力,难度适中.

练习册系列答案
相关题目


 =?
=?