题目内容
如图所示，绝缘板MN上有一小孔D，DM长度为L．MN上方有场强为E的匀强电场，电场方向竖直向下，绝缘板MN上下方有磁感应强度相同的匀强磁场，方向垂直纸面向外．MN下方是磁场的边界线MP与板MN成30°角的有界磁场．ab是一根长度为L绝缘细杆，沿电场线放置在小孔的正上方的场中，b端恰在D处．将一套在杆上的带正电的小球从a端由静止释放后，小球先做加速运动，后做匀速运动到达b端，再从缺口处进入，小球进入MN下方磁场后圆周运动轨迹恰与MP相切，已知小球与绝缘杆间的动摩擦因数为μ=0.3，小球重力忽略不计．小球与板MN接触后不再反弹．求此带电小球从a端由静止释放后运动到达b端过程中电场力所做的功W电与克服摩擦力所做的功Wf的比值．
分析：根据小球在杆上匀速运动受力平衡，可求得电场表达式，作出小球在下方磁场中的轨迹图，结合几何关系可求得小球的速度
利用电场力做功和动能定理联立可求得电场力做功和摩擦力做功的表达式，从而可求得二者之比．
利用电场力做功和动能定理联立可求得电场力做功和摩擦力做功的表达式，从而可求得二者之比．
解答：解：小球在杆上匀速运动时受力分析如图1所示，设小球在杆上匀速运动的速度为v，磁感应强度为B，电量是q，根据共点力平衡有：
F电=qE=f 摩
F洛=qvB=N 压
而 f 摩=μN压
由以上几式解得：qE=μqvB，得：E=μvB
小球进入下方磁场后圆周运动轨迹恰与MP相切，轨迹圆的圆心为O，如图2所示．
由几何关系有：2r=L-r
解得轨迹圆半径r=
L
又由：qvB=
得：v=
小球从a到b过程中，W电-Wf=
mv2
W电=qEL=qμvBL=
=
Wf=W电-
mv2=
故可得：W电：Wf=9：4
答：电场力所做的功W电与克服摩擦力所做的功Wf的比值为9：4．
F电=qE=f 摩
F洛=qvB=N 压
而 f 摩=μN压
由以上几式解得：qE=μqvB，得：E=μvB
小球进入下方磁场后圆周运动轨迹恰与MP相切，轨迹圆的圆心为O，如图2所示．
由几何关系有：2r=L-r
解得轨迹圆半径r=
| 1 |
| 3 |
又由：qvB=
| mv2 |
| r |
| qBL |
| 3m |
小球从a到b过程中，W电-Wf=
| 1 |
| 2 |
W电=qEL=qμvBL=
| μq2B2L2 |
| 3m |
| q2B2L2 |
| 10m |
Wf=W电-
| 1 |
| 2 |
| q2B2L2 |
| 22.5m |
故可得：W电：Wf=9：4
答：电场力所做的功W电与克服摩擦力所做的功Wf的比值为9：4．
点评：本题关键明确小球匀速运动时的受力状态及在磁场中运动的轨迹，结合几何关系，根据功的公式和动能定理的综合应用，综合性强．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
如图所示，MN是一固定在水平地面上足够长的绝缘平板（左侧有挡板），整个空间有方向平行于平板向右，大小E=10N/C的匀强电场，在板上C点的左侧有一个垂直于纸面向外、大小B=5T的匀强磁场．一个质量m=0.5kg，带电量q=-0.2C的小物块从C点由静止开始向左先做加速运动再做匀速运动并与左端挡板碰撞后被弹回．若在碰撞瞬间将电场改为竖直向下、大小不变，小物块被挡板弹回时在磁场中恰能做匀速运动．已知平板MC部分的长度为L=5m，物块与平板间的动摩擦因数为μ=0.2，g取10m/s2．求：（1）小物块在磁场中向左做匀速运动的速度；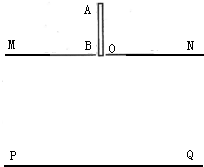
如图所示，MN、PQ为水平放置、相距为d的两平行金属板，两板间电压为U，且上板带正电，板MN中央有一个小孔0，板间电场可认为匀强电场．AB是一根长为L（L＜d）、质量为m的均匀带负电的绝缘细杆．现将杆下端置于O处，然后将杆由静止释放，杆运动过程中始终保持竖直．当杆下落
（2010?苏州二模）如图所示，间距为L的平行金属板AB、CD之间有相互垂直的匀强电场和匀强磁场（图中未画出），电场强度为E1，磁感应强度为B1．带异种电荷的两离子a、b，负离子a质量为m、带电量为q，其比荷为正离子b比荷的9倍．它们在分别距离AB、CD板L/4处，以平行于金属板方向的速度沿直线穿过ABCD区域进入电场强度为E2的匀强电场区，E2与E1平行．MNP为沿AB、CD中心线方向的光滑绝缘板，离子与板碰撞后反弹无能量损失（即反弹前后水平分速度保持不变，竖直分速度大小不变、方向相反），且电量保持不变，到达板的N点后反弹进入磁感应强度为B2的匀强磁场区，不计两离子间的相互作用力及重力．