题目内容
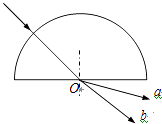
【题目】半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率为 n= ![]()
①求红光在玻璃中的传播速度为多大?
②求两条光线经圆柱面和底面折射后的交点与O点的距离d.
【答案】解:①由n= ![]() 得:v=
得:v= ![]() =
= ![]() =
= ![]() ×108m/s≈1.73×108m/s
×108m/s≈1.73×108m/s
②如图所示,光线1通过玻璃砖后不偏折.光线2入射角 i=60°.
由n= ![]() 得:sinr=
得:sinr= ![]() =
= ![]() ,r=30°,
,r=30°,
由几何知识得:i′=60°﹣r=30°.
由 n= ![]() 得:sinr′=nsini′=
得:sinr′=nsini′= ![]() ,r′=60°,
,r′=60°,
由正弦定理,得:OC= ![]() R,
R,
则d=OCtan 30°= ![]() R.
R.
答:①红光在玻璃中的传播速度为1.73×108m/s.
②两条光线经圆柱面和底面折射后的交点与O点的距离d是 ![]() R.
R.

【解析】①已知折射率n,根据公式v= ![]() 求红光在玻璃中的传播速度.②光线1通过玻璃砖后不偏折.光线2在圆柱面上的入射角为60°,根据折射定律求出折射角,由几何知识求出在底面上的入射角,再由折射定律求出折射角,作出光路图.根据几何关系求解d.
求红光在玻璃中的传播速度.②光线1通过玻璃砖后不偏折.光线2在圆柱面上的入射角为60°,根据折射定律求出折射角,由几何知识求出在底面上的入射角,再由折射定律求出折射角,作出光路图.根据几何关系求解d.
【考点精析】根据题目的已知条件,利用光的折射的相关知识可以得到问题的答案,需要掌握光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目