题目内容
 如图所示,在光滑的桌面上叠放着一质量为mA=2Kg的薄木板A和质量为mB=3Kg的金属块B.A的长度l=2m.B上有轻线绕过定滑轮与质量为mC=1Kg的物块C相连,B与A间的动摩擦因素μ=0.1,最大静摩擦力可视为等于滑动摩擦力.忽略滑轮质量及与轴间的摩擦,开始时各物体都处于静止状态,绳被拉直,B位于A的左端,然后放手.求经过多长时间后B从A的右端脱离(设A的右端距滑轮足够远)(g取10m/s2).
如图所示,在光滑的桌面上叠放着一质量为mA=2Kg的薄木板A和质量为mB=3Kg的金属块B.A的长度l=2m.B上有轻线绕过定滑轮与质量为mC=1Kg的物块C相连,B与A间的动摩擦因素μ=0.1,最大静摩擦力可视为等于滑动摩擦力.忽略滑轮质量及与轴间的摩擦,开始时各物体都处于静止状态,绳被拉直,B位于A的左端,然后放手.求经过多长时间后B从A的右端脱离(设A的右端距滑轮足够远)(g取10m/s2).分析:根据牛顿第二定律分别求出A、B的加速度,结合运动学公式,抓住位移之差等于A的长度,求出BB从A的右端脱离的时间.
解答:解:根据牛顿第二定律得,B的加速度aB=
=
=
m/s2.
A的加速度aA=
=
m/s2.
根据
aBt2-
aAt2=l
解得t=4s.
答:经过4s时间后B从A的右端脱离.
| mCg-μmBg |
| mB+mC |
| 10-3 |
| 4 |
| 7 |
| 4 |
A的加速度aA=
| μmBg |
| mA |
| 3 |
| 2 |
根据
| 1 |
| 2 |
| 1 |
| 2 |
解得t=4s.
答:经过4s时间后B从A的右端脱离.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解.注意整体法和隔离法的运用.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
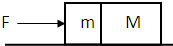 如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )| A、F | ||
B、
| ||
C、若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力为
| ||
D、若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力仍为
|
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为:( )
A. |
B. |
C.若桌面的摩擦因数为 ,M、m仍向右加速,则M、m间的相互作用力为 ,M、m仍向右加速,则M、m间的相互作用力为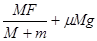 |
D.若桌面的摩擦因数为 ,M、m仍向右加速,则M、m间的相互作用力为 ,M、m仍向右加速,则M、m间的相互作用力为 |
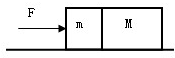 如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )


 ,M、m仍向右加速,则M、m间的相互作用力为
,M、m仍向右加速,则M、m间的相互作用力为
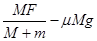



 ,M、m仍向右加速,则M、m间的相互作用力为
,M、m仍向右加速,则M、m间的相互作用力为