题目内容
（2011?宜兴市模拟）2007年10月24日，我国第一颗探月卫星“嫦娥一号”成功发射，标志着我国航天事业取得巨大成就．卫星发射后，假设地-月转移轨道阶段可以简化为：绕地球做匀速圆周运动的卫星，在适当的位置P点火，进入Q点后被月球俘获绕月球做匀速圆周运动，已知月球表面重力加速度为g，月球半径为R，“嫦娥一号”绕月球做匀速圆周运动的轨道半径为r，从发射“嫦娥一号”到在绕月轨道上正常运行，其示意图如图所示，则下列说法正确的是（ ）分析：“嫦娥一号”在P点变轨时，启动火箭向后喷气，使之做离心运动．在Q点启动火箭向运动方向喷气，使之做向心运动．“嫦娥一号”在绕月轨道上运行时，由月球的万有引力提供向心力，由牛顿第二定律得到“嫦娥一号”在绕月轨道上运行的速率表达式，再由万有引力等于重力，求出月球的质量，联立求解速率．
解答：解：
A、“嫦娥一号”在P点变轨时，启动火箭向后喷气，使之做离心运动，才能逐渐脱离地球的引力束缚．故A错误．
B、在Q点启动火箭向运动方向喷气，使“嫦娥一号”做向心运动，才能使之到在绕月轨道上运行．故B正确．
C、D设月球的质量为M，卫星的质量为m，“嫦娥一号”在绕月轨道上运行时，由月球的万有引力提供向心力，则有
G
=m
，
又G
=mg，联立解得，v=
．故C错误，D正确．
故选BD
A、“嫦娥一号”在P点变轨时，启动火箭向后喷气，使之做离心运动，才能逐渐脱离地球的引力束缚．故A错误．
B、在Q点启动火箭向运动方向喷气，使“嫦娥一号”做向心运动，才能使之到在绕月轨道上运行．故B正确．
C、D设月球的质量为M，卫星的质量为m，“嫦娥一号”在绕月轨道上运行时，由月球的万有引力提供向心力，则有
G
| Mm |
| r2 |
| v2 |
| r |
又G
| Mm |
| R2 |
|
故选BD
点评：本题中卫星变轨时，可根据卫星所需要的向心力和提供的向心力关系分析火箭应加速还是减速．公式g=
反映了重力加速度与月球质量的关系，是常常隐含的方程式．
| GM |
| R2 |
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
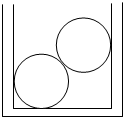（2011?宜兴市模拟）直径为D的圆柱形桶内放入两个直径为d（2d＞D）的光滑圆球，如图所示，其中只与球的重力有关而与桶的直径D无关的力是（ ）
（2011?宜兴市模拟）一个机要仓库有一扇很大的电动仓库门，门上装有三把锁，三个机要员各有一把锁的钥匙，只有三人同时转动自己的钥匙（闭合自己的开关），才能通过一个继电器把门打开．图中的S1、S2、S3是三个锁内的开关，J为继电器（图中未画电动机的电路）．则方框内符合要求的门电路是（ ）
（2011?宜兴市模拟）酒精测试仪用于对机动车驾驶人员是否酒后驾车及其他严禁酒后作业人员的现场检测，它利用的是一种二氧化锡半导体型酒精气体传感器．酒精测试仪的工作原理如图所示，其中P是半导体型酒精气体传感器，该传感器电阻r′的倒数与酒精气体的浓度C成正比，R0为定值电阻．以下关于电压表示数的倒数与酒精气体浓度的倒数之间关系的图象，正确的是（ ）