题目内容
如图所示，横截面是直角三角形ABC的三棱镜对红光的折射率为n1，对紫光的折射率为n2．一束很细的白光由棱镜的一个侧面AC折射出来，已知棱镜顶角∠A＝30°，AC边平行于光屏MN，且与光屏的距离为L．
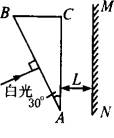
（1）画出白光通过棱镜折射的光路图．（出射光线只画出两条边缘光线，并指明其颜色）
（2）求在光屏MN上得到的可见光光谱的宽度d．
答案：
解析：
解析：
解析：由于光线垂直AB面入射，故在 AB面上光线不偏折． 在AC面，入射角为30°．设红光折射角为β1，紫光折射角为β2．由于n2＞n1，紫光偏折角度将大于红光，故β2＞β1，光谱上方为紫光，下方为红光． 由折射定律有 n1sin30°＝sinβ1 n2sin30°＝sinβ2 则sinβ1＝ MN上可见光谱的宽度 d＝L（tanβ2－tanβ1） ＝L（ ＝L（ 说明：本题涉及到的知识较多，如：棱镜对光的偏折问题，不同色光偏折角不同，折射定律，几何关系等．要理清这些知识间的关系，并能熟练地运用它们，才能顺利解出这类题目． |
，sinβ2＝
．
－
）
-
）．
练习册系列答案
相关题目
电磁流量计广泛应用于测量可导电流体（如污水）在管中的流量（在单位时间内通过管内横截面的流体的体积）．为了简化，假设流量计是如图所示的横截面为长方形的一段管道，长、宽、高分别为图中的a、b、c表示，左右两端开口，流量计的两端与输送流体的管道相连接．图中流量计的前后两面是金属材料，上下两面是绝缘材料．现于流量计所在处加竖直向下磁感应强度为B的匀强磁场，在管外将流量计前后两表面用导线串接一电阻R和电流表，当流体匀速流经流量计时，电流表读数为I．已知流体的电阻率为ρ，不计电流表的内阻，则流体的流量Q可表示为（ ）
如图所示，横截面为直角三角形斜劈A，放在粗糙的水平地面上，在劈与竖直墙壁之间放置一光滑球B，系统处于静止状态．在球B上施一通过球心的力F，系统仍保持静止，下列说法正确的是（ ）
（2011?吉安模拟）〔物理--选修3-4〕
砖的折射率为n（n＜2），不考虑光在OA、OB面的反射．问：