题目内容
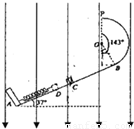
如图所示，一弹簧在倾角为θ的斜面上，下端固定，上端连接质量为m的滑块A，用一锁定K将A锁定在斜面上，并使弹簧刚好处于原长．在A点之下段斜面光滑，在A点之上段斜面粗糙．现将质量也为m的物块B从距离A为L的P点以某一初速度滑下，当B刚要与A相碰瞬间锁定K立即自动解开，使B与A相碰（相碰时间极短），并使A、B以共同的速度压缩弹簧（A、B互不粘连），然后B又刚好被反弹回P点而速度减为零．B物块与粗糙段摩擦因数为μ．求B物原来的初速度大小．分析：B下滑过程中有重力及摩擦力做功，由动能定理可得出表达式；而在AB碰撞中动量守恒，由动量守恒定律可得出表达式；再对AB分离后对B分析，由动能定理可得出表达式，联立可解．
解答：解：设B物块的初为V0，B与A碰前瞬间的速度为V1，B与A碰后的瞬间的速度为V2，对B在碰前过程有：
mgLsinθ-μmgLcosθ=
mV12-
mV22
A、B碰撞动量守恒：m V1=2m V2
A、B反弹后在弹簧的原长分离，对B分离后有：mgLsinθ+μmgLcosθ=
mV22
由上三式可解得：V1=
答：B物体原来的初速度为
mgLsinθ-μmgLcosθ=
| 1 |
| 2 |
| 1 |
| 2 |
A、B碰撞动量守恒：m V1=2m V2
A、B反弹后在弹簧的原长分离，对B分离后有：mgLsinθ+μmgLcosθ=
| 1 |
| 2 |
由上三式可解得：V1=
| 2gL(3sinθ+5μcosθ |
答：B物体原来的初速度为
| 2gL(3sinθ+5μcosθ |
点评：对于动能定理的应用题目，一定要注意分析过程，对不同的过程分别应用动能定理或动量守恒列式，注意各过程之间的联系，联立方程可解．
练习册系列答案
相关题目
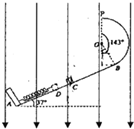如图所示，AB为倾龟θ=37°的绝缘直轨道，轨道的AC部分光滑，CB部分粗糙．BP为半径R=1.0m的绝缘竖直光滑圆弧形轨道，O为圆心，圆心角∠BOP=143°、两轨道相切于B点，P、O两点在同一竖直线上．轻弹簧下端固定在A点上端自由伸展到C点，整个装置处在竖直向下的足够大的匀强电场中，场强E=1.0×106N/C．现有一质量m=2.0kg、带负电且电量大小恒为q=1.0×10-5C的物块（视为质点），靠在弹簧上端（不拴接），现用外力推动物块，使弹簧缓慢压缩到D点，然后迅速撤去外力，物块被反弹到C点时的速度VC=10m/So物块与轨道CB间的动摩擦因素μ=0.50，C、D间的距离L=1．Om5物块第一次经过B点后恰能到P点．（sin37°=0.6，cos37°=0.8，g 取 10m/s2） 