��Ŀ����
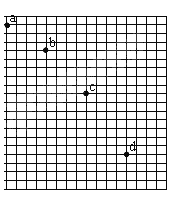
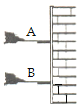
����Ŀ����ͼ��ʾ����ˮƽƽ̨����һ����m=0.1kg��С��ѹ�����ʵ��ɣ�С���뵯�ɲ�˨������A�㣬ƽ̨��B�����Ӱ뾶ΪR=0.2m���ڱڹ⻬�Ķ���֮һϸԲ��BC��Բ���ھ��Դ���С��ֱ����С�����Ϊ�ʵ㣬B���C�㶼��ˮƽ�����С��ڵ����D�㰲װ��һ���ɱ���ǵ��㹻��б��DE����֪����CD��Ϊ![]() ����С�������֮��Ķ�Ħ������
����С�������֮��Ķ�Ħ������![]() ��С����ɶ�б��DE��Ķ�Ħ������
��С����ɶ�б��DE��Ķ�Ħ������![]() �����ͷ�С��С�������ϸԲ�ܣ��˶���C��ʱ�ٶȴ�СΪ
�����ͷ�С��С�������ϸԲ�ܣ��˶���C��ʱ�ٶȴ�СΪ![]() ��
�� ![]() ����
����

��1��С��C��ʱ�Թܱڵ���������
��2����б��EF�����ļн�![]() ����0~90����Χ�ڣ�Ϊ��ֵʱ��С����б���ϻ��ij�����̲���������̳��ȣ�С��D��ʱ�ٶȴ�С���䣩��
����0~90����Χ�ڣ�Ϊ��ֵʱ��С����б���ϻ��ij�����̲���������̳��ȣ�С��D��ʱ�ٶȴ�С���䣩��
���𰸡�(1) ![]() (2)
(2) ![]()
����������1����С����C���ܵ���֧����ΪN��С��Թܱڵ�ѹ��Ϊ![]()
������C��![]() ��
��
���N=13.5N��
����ţ�ٵ������ɿɵ�![]()
��2����С����D����ٶ�Ϊ![]() ��С���D����E�����ߵ�֮�����Ϊs��С���C�㵽D����
��С���D����E�����ߵ�֮�����Ϊs��С���C�㵽D���� ![]() ��
��
���![]()
С����DEб���ϣ� ![]() ��
��
С����б���ϵ�λ��![]() ��
��
�ɢ٢ڿɵ�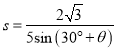
��![]() ʱ��s��С��
ʱ��s��С�� ![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ