题目内容
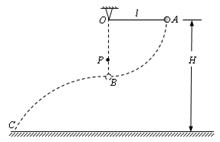
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.40kg的小球,悬点O距离水平地面的高度H=1.60m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,速度大小vB=2.0m/s,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
(1)绳断裂后球从B点抛出并落在水平地面的C点,求C点与B点之间的距离;
(2)若轻绳所能承受的最大拉力Fm=12.0N.欲使轻绳断裂,钉子P与O点的距离d应满足什么条件?
(1)绳断裂后球从B点抛出并落在水平地面的C点,求C点与B点之间的距离;
(2)若轻绳所能承受的最大拉力Fm=12.0N.欲使轻绳断裂,钉子P与O点的距离d应满足什么条件?

(1)小球从B点做平抛运动,设C点与B点之间的水平距离为x,
水平方向:x=vBt,
竖直方向:H-l=
gt2
解得:x=0.80m,
C点与B点之间的距离s=
,解得 s=
m.
(2)若轻绳碰到钉子时,轻绳拉力恰好达到最大值Fm,
由牛顿定律得Fm-mg=m
,
由几何关系得:r=l-d,
由以上两式解得:d=0.60m,
因此钉子P与O点的距离d应满足条件d>0.60m.
答:(1)C点与B点之间的距离为
m;
(2)欲使轻绳断裂,钉子P与O点的距离d>0,60m.
水平方向:x=vBt,
竖直方向:H-l=
| 1 |
| 2 |
解得:x=0.80m,
C点与B点之间的距离s=
| x2+(H-l)2 |
| 4 |
| 5 |
| 2 |
(2)若轻绳碰到钉子时,轻绳拉力恰好达到最大值Fm,
由牛顿定律得Fm-mg=m
| ||
| r |
由几何关系得:r=l-d,
由以上两式解得:d=0.60m,
因此钉子P与O点的距离d应满足条件d>0.60m.
答:(1)C点与B点之间的距离为
4
| ||
| 5 |
(2)欲使轻绳断裂,钉子P与O点的距离d>0,60m.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.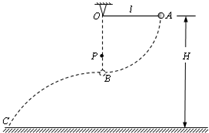 一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.40kg的小球,悬点O距离水平地面的高度H=1.60m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,速度大小vB=2.0m/s,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.40kg的小球,悬点O距离水平地面的高度H=1.60m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,速度大小vB=2.0m/s,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2. (2013?丰台区一模)一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.求:
(2013?丰台区一模)一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.求: 一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.绳断裂后球从B点抛出并落在水平地面的C点,不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.绳断裂后球从B点抛出并落在水平地面的C点,不计轻绳断裂的能量损失,取重力加速度g=10m/s2.