题目内容
【题目】质量为![]() 的小滑块(可视为质点)放在质量为
的小滑块(可视为质点)放在质量为![]() 的木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为
的木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为![]() ,木板长
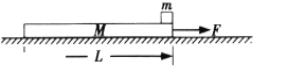
,木板长![]() 。开始时两者都处于静止状态,现对木板施加水平向右的恒力
。开始时两者都处于静止状态,现对木板施加水平向右的恒力![]() ,如图所示,经一段时间后撤去
,如图所示,经一段时间后撤去![]() ,小滑块始终在木板上。
,小滑块始终在木板上。![]() 取
取![]() 。
。
(1).求撤去外力前后木板的加速度的大小和方向;
(2).设经过时间![]() 撤去外力,试画出木板从开始运动到停止过程中的速度一时间图象;
撤去外力,试画出木板从开始运动到停止过程中的速度一时间图象;
(3).求水平恒力![]() 作用的最长时间。
作用的最长时间。
(4).变式:若小滑块与木板间的动摩擦因数为![]() ,地面光滑,水平恒力
,地面光滑,水平恒力![]() 作用的最长时间是多少?
作用的最长时间是多少?
【答案】(1)撤力前: ![]() ,方向向右 ;撤力后:
,方向向右 ;撤力后: ![]() ,方向向左。
,方向向左。
(2)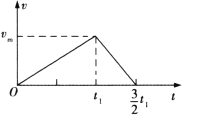 (3)
(3)![]() ;(4)
;(4)![]()
【解析】
根据牛顿第二定律列出撤去外力之前和撤去之后的方程,联立即可解得撤去外力前后木板的加速度的大小和方向;由于减速过程加速度的大小为加速过程的两倍,所以加速时间为t1,则再经t1/2,木板的速度就减小为零,即可做出速度—时间图象;木板先加速后减速运动,设加速过程的位移为![]() ,加速运动的时间为
,加速运动的时间为![]() ,减速过程的位移为
,减速过程的位移为![]() ,减速运动的时间为
,减速运动的时间为![]() ,结合位移间的关系即可求出力
,结合位移间的关系即可求出力![]() 作用的最长时间;撤力前木板和小滑块都做加速运动,且木板的加速度较大,所以撤力时木板的速度较大。撤去外力后由于木板速度较大,所以小滑块继续做加速运动,而木板做减速运动。根据牛顿第二定律、运动学公式和位移间的关系即可求出水平恒力
作用的最长时间;撤力前木板和小滑块都做加速运动,且木板的加速度较大,所以撤力时木板的速度较大。撤去外力后由于木板速度较大,所以小滑块继续做加速运动,而木板做减速运动。根据牛顿第二定律、运动学公式和位移间的关系即可求出水平恒力![]() 作用的最长时间。
作用的最长时间。
(1)由牛顿第二定律得,撤去外力之前:![]()
代入数据解得:![]() 方向向右
方向向右
撤力后:![]()
代入数据解得:![]() 方向向左
方向向左
(2)由于减速过程加速度的大小为加速过程的两倍,所以加速时间为![]() ,则再经
,则再经![]() ,木板的速度就减小为零。其速度—时间图象如图所示:
,木板的速度就减小为零。其速度—时间图象如图所示:

(3)木板先加速后减速运动,设加速过程的位移为![]() ,加速运动的时间为
,加速运动的时间为![]() ,减速过程的位移为
,减速过程的位移为![]() ,减速运动的时间为
,减速运动的时间为![]() 。
。
由运动学规律有![]()
![]()
小滑块始终在木板上应满足![]()
又![]()
由以上各式可解得![]() ,即力
,即力![]() 作用的最长时间为
作用的最长时间为![]()
(4)撤力前木板和小滑块都做加速运动,且木板的加速度较大,所以撤力时木板的速度较大。撤去外力后由于木板速度较大,所以小滑块继续做加速运动,而木板做减速运动。设木板加速过程的位移为![]() ,加速度大小为
,加速度大小为![]() ,加速运动的时间为
,加速运动的时间为![]() ,减速过程的位移为
,减速过程的位移为![]() ,加速度大小为
,加速度大小为![]() ,减速运动的时间为
,减速运动的时间为![]() ;整个过程中小滑块运动的加速度为
;整个过程中小滑块运动的加速度为![]()
由牛顿第二定律得:![]()
解得:![]()
撤力前:![]()
解得:![]()
撤力后:![]()
解得:![]()
撤力时刻,木板的速度:![]() ,
,
运动的位移: ![]()
最终木板的速度为![]()
减速运动过程中木板的位移:![]()
最终小滑块的速度为:![]()
全过程中小滑块运动的位移为:![]() ,
,
小滑块始终在木板上,应满足:![]()
又![]()
由以上各式可解得![]() ,即力
,即力![]() 作用的最长时间为
作用的最长时间为![]() 。
。

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案