Question

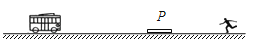
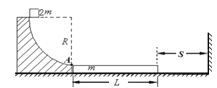
【题目】（14分）如图所示，一个质量为m的长木板静止在光滑的水平面上，并与半径为的光滑圆弧形固定轨道接触（但不粘连），木板的右端到竖直墙的距离为s；另一质量为2m的小滑块从轨道的最高点由静止开始下滑，从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。已知滑块与长木板间的动摩擦因数为μ。试求：

（1）滑块到达A点时的速度大小以及物体对轨道的压力大小；

（2）若滑块不会滑离长木板，试讨论长木板与墙第一次碰撞前的速度与s的关系；

（3）若s足够大，为了使滑块不滑离长木板，板长L应满足什么条件。

Answer 1

【答案】（1）6mg；（2）若，则木板与墙第一次碰前瞬间的速度为；若，则木板与墙第一次碰前瞬间的速度为 ；（3）。

【解析】

试题（1）滑块从轨道的最高点到最低点，由机械能守恒，

设到达A点的速度为；则①

得：②

由牛顿第二定律可知，在A点有：③

由②③得：④

由牛顿第三定律，滑块在A点对轨道的压力：⑤

（2）若第一次碰撞前的瞬间，滑块与木板达到共同速度，

则：⑥

⑦

由②⑥⑦得：⑧

ⅰ.若,则木板与墙第一次碰前瞬间的速度为⑨

ⅱ. 若,则木板与墙第一次碰前瞬间的速度为，则:⑩

得: 11

（3）因为S足够大，每次碰前滑块与木板共速；因为，每次碰后系统的总动量方向向右，要使滑块不滑离长木板，最终木板停在墙边，滑块停在木板上。（没有文字说明的扣1分）

由能量守恒得:12，

解得13

评分标准:①⑥⑦每式2分，123分，其余每式1分。