Question

如图所示，在光滑的圆锥顶用长为l的细线悬挂一质量为m的小球，圆锥体固定在水平面上不动，其轴线沿竖直方向，母线与轴线之间的夹角为30°，物体以速率v绕圆锥体轴线做水平匀速圆周运动：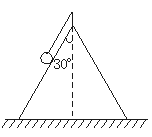

（1）当v₁＝时，求绳对物体的拉力；

（2）当v₂＝时，求绳对物体的拉力．

Answer 1

答案：
解析：

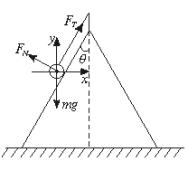
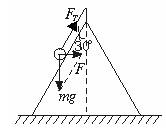
解析：当物体的速率较小时，物体在圆锥面上运动，受到重力mg，绳的拉力FT和圆锥面的弹力FN作用；当物体速率v超过某个数值时，物体将和锥体表面脱离接触，此时物体只受重力mg和绳的拉力FT作用；本题的关键是先求出物体和锥面接触的最大速率v0，然后比较v1、v2和v0的大小确定物体所受的力． 如图所示，物体在锥面上运动，但FN＝0，物体只受重力mg和绳的拉力FT作用，其合力应沿水平面指向轴线，由图可知： F＝mgtanθ                                                                                                            ① 根据牛顿第二定律有： F＝ma＝m＝m                                                                                      ② 由①②两式解得： v0＝ （1）因为v1＜v0，所以物体与锥面接触并产生弹力FN，此时物体受力如图所示． 根据牛顿第二定律有： FTsinθ－FNcosθ＝                                                                            ③ FTcosθ＋FNsinθ－mg＝0                                                                               ④ 解得：FT＝ （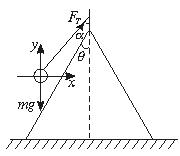2）因为v2＞v0，所以物体与锥面脱离接触，设绳与竖直方向的夹角为a，此时物体受力如图所示． 根据牛顿第二定律有： FTsina＝                                                                                             ⑤ FTcosa－mg＝0                                                                                               ⑥ 由⑤⑥两式解得：FT＝2mg

提示：