题目内容
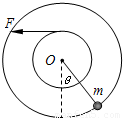半径分别为r和2r的两个质量不计的圆盘，共轴固定连接在 一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有 一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O的正下方位置．现以水平恒力F拉细绳，使两圆盘转动，若恒力 F=mg，两圆盘转过的角度θ= 时，质点m的速度最大．若圆盘转过的最大角度θ=π/3，则此时恒力F= ．
【答案】分析：当F的力矩大于mg的力矩时，质点m的速度增大，当F的力矩小于mg的力矩时，质点m的速度减小，则当两者力矩相等时，质点m的速度最大．根据力矩平衡条件列方程求解．再能量守恒定律求解F．
解答：解：当F的力矩等于mg的力矩时，质点m的速度最大．
则有Fr=mg?2rsinθ
又F=mg
解得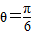
根据能量守恒定律得
F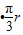
=mg
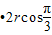
解得F=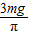
本题答案是：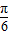
，
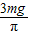
点评：本题解题关键在于分析什么时候质点的速度最大，要根据力矩的作用使物体产生转动来分析．
解答：解：当F的力矩等于mg的力矩时，质点m的速度最大．
则有Fr=mg?2rsinθ
又F=mg
解得
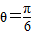
根据能量守恒定律得
F
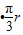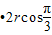
=mg解得F=
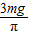
本题答案是：
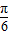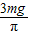
，点评：本题解题关键在于分析什么时候质点的速度最大，要根据力矩的作用使物体产生转动来分析．
练习册系列答案
相关题目
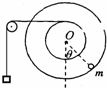半径分别为r和2r的两个质量不计的圆盘，共轴固定连结在 一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个质量为m的质点，小圆盘上绕有细绳，绳的另一端通过一个可绕光滑水平轴转动的轻定滑轮悬挂一个质量也为m的物体．开始时托住物体让圆盘静止，质点处在水平轴O的正下方位置．放开物体，两圆盘转动，当两圆盘转过的角度θ时，质点m的速度为
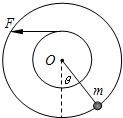（2006?上海）半径分别为r和2r的两个质量不计的圆盘，共轴固定连接在 一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有 一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O的正下方位置．现以水平恒力F拉细绳，使两圆盘转动，若恒力 F=mg，两圆盘转过的角度θ=
如图的环状轨道处于竖直面内，它由半径分别为R和2R的两个半圆轨道、半径为R的两个四分之一圆轨道和两根长度分别为2R和4R的直轨道平滑连接而成．以水平线MN和PQ为界，空间分为三个区域，区域Ⅰ和区域Ⅲ有磁感应强度为B的水平向里的匀强磁场，区域Ⅰ和Ⅱ有竖直向上的匀强电场．一质量为m、电荷量为+q的带电小环穿在轨道内，它与两根直轨道间的动摩擦因数为μ（0＜μ＜1），而轨道的圆弧形部分均光滑．将小环在较长的直轨道CD下端的C点无初速释放（已知区域Ⅰ和Ⅱ的匀强电场场强大小为E=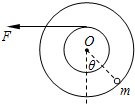
半径分别为r和2r的两个质量不计的圆盘，共轴固定连结在一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O的正下方位置．现以水平恒力F拉细绳，使两圆盘转动，若两圆盘转过的角度θ=
如图所示，Q是真空中固定的点电荷，a、b、c是以Q所在位置为圆心、半径分别为r和2r的球面上的三点．将电荷量为q1、q2的检验正电荷分别从a、c两点移至无穷远处，已知两电荷的电势能均增大且增量相同．不计q1、q2的相互作用，下列判断正确的是（ ）| A、Q带负电 | B、b、c两点电场强度相同 | C、a、b两点的电场强度的大小之比为4：1 | D、q1＞q2 |