题目内容
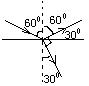
一束光由空气入射入某介质,入射角为60°,其折射光线恰好与反射光线垂直,则光在该介质中的传播速度为( )
分析:入射光线与界面的夹角为30°,根据光的反射定律,就会算出入射角,也就知道反射角的度数,反射光线与折射光线恰好垂直,再根据折射角等于180°减去反射光线与折射光线的夹角和反射角.根据折射定律n=
求出折射率n,由v=
求光在该介质中的传播速度.
| sini |
| sinr |
| c |
| n |
解答:解:由题意,入射角为:i=60°,
又因为反射角等于入射角,所以反射角为i′=60°,
因为反射光线与折射光线的夹角等于90°,
所以反射角与折射角之和等于90°,
故折射角为:r=180°-90°-60°=30°.
则得折射率n=
=
光在该介质中的传播速度v=
=
m/s=
×108m/s
故选B
又因为反射角等于入射角,所以反射角为i′=60°,
因为反射光线与折射光线的夹角等于90°,
所以反射角与折射角之和等于90°,
故折射角为:r=180°-90°-60°=30°.
则得折射率n=
| sini |
| sinr |
| 3 |
光在该介质中的传播速度v=
| c |
| n |
| 3×108 | ||
|
| 3 |
故选B
点评:本题考查反射定律和折射定律的应用,该类型题的关键是牢记反射定律内容和折射定律内容.

练习册系列答案
相关题目