题目内容
 如图所示,水平方向的有界匀强磁场区域高度为d,三个宽度均为d的由相同导线制成的闭合导线框竖直置于磁场的上方,它们的底边处在同一高度,线框的高度hA=d/2,hB=d,hC=3d/2.当导线框A、B、C由静止开始释放后,在经过匀强磁场的过程中线框受到的磁场力始终小于线框的重力,则( )
如图所示,水平方向的有界匀强磁场区域高度为d,三个宽度均为d的由相同导线制成的闭合导线框竖直置于磁场的上方,它们的底边处在同一高度,线框的高度hA=d/2,hB=d,hC=3d/2.当导线框A、B、C由静止开始释放后,在经过匀强磁场的过程中线框受到的磁场力始终小于线框的重力,则( )分析:线框下落过程,机械能均守恒,可知刚进入磁场时三个导线框的速度相同.推导出安培力的表达式,根据牛顿第二定律分析加速度关系.当穿过线框的磁通量不变化时,没有感应电流产生.由运动学公式分析导线框进入磁场后,位移小于
以前,经相等位移时导线框速度关系.
| d |
| 2 |
解答:解:A、线框下落过程进入磁场前,机械能均守恒,根据机械能守恒定律得 mgh=
mv2,得v=
,可知刚进入磁场时三个导线框的速度相同.故A正确.
B、线框进入磁场
后,线框完全进入磁场中,没有感应电流,不受安培力,加速度等于g,而BC仍有感应电流,受到向上的安培力,则它们的加速度小于g,故线框A的加速度最大.故B错误.
C、设线框的截面积为S,高度为h,电阻率为ρ1,电阻为R,密度为ρ2,则根据牛顿第二定律得,线框进入磁场后加速度为
a=
=g-
=g-
=g-
,则知,线框的高度越大,加速度越大,则线框进入磁场
后,导线框C的加速度最大,当线框A刚无感应电流时速度最小,没有感应电流时三个线框的加速度为g,A、C线框通过的位移相同,均为
,B一直有感应电流,则通过磁场过程中无感应电流的时间导线框A最长.故C正确.
C、由上分析得知,c线框进入磁场后加速度最大,经相等位移时导线框C的速度最大.故D正确.
故选ACD
| 1 |
| 2 |
| 2gh |
B、线框进入磁场
| d |
| 2 |
C、设线框的截面积为S,高度为h,电阻率为ρ1,电阻为R,密度为ρ2,则根据牛顿第二定律得,线框进入磁场后加速度为
a=
| mg-FA |
| m |
| ||
| m |
| B2d2v | ||
ρ1
|
| B2d2v |
| 4ρ1ρ2(d+h)2 |
| d |
| 2 |
| d |
| 2 |
C、由上分析得知,c线框进入磁场后加速度最大,经相等位移时导线框C的速度最大.故D正确.
故选ACD
点评:本题的难点是分析三个线框进入磁场后加速度关系,要综合考虑质量、电阻等因素,由牛顿第二定律进行分析.此题综合性很强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?上海模拟)如图所示,水平方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5 C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线
(2010?上海模拟)如图所示,水平方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5 C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线 如图所示,水平方向的匀强电场和匀强磁场互相垂直,竖直的绝缘杆足够长,杆上套一带电小环,小环和竖直杆都不光滑,小环由静止开始下落的过程中( )
如图所示,水平方向的匀强电场和匀强磁场互相垂直,竖直的绝缘杆足够长,杆上套一带电小环,小环和竖直杆都不光滑,小环由静止开始下落的过程中( ) 如图所示,水平方向的匀强电场的场强为E,场区宽度为L,紧挨着电场的是垂直纸面向外的两个匀强磁场区域,其磁感应强度分别为B和2B,三个场的竖直方向均足够长.一个质量为m,电量为q的带正电粒子,其重力不计,从电场的边界MN上的a点由静止释放,经电场加速后进人磁场,穿过中间磁场所用的时间t0=
如图所示,水平方向的匀强电场的场强为E,场区宽度为L,紧挨着电场的是垂直纸面向外的两个匀强磁场区域,其磁感应强度分别为B和2B,三个场的竖直方向均足够长.一个质量为m,电量为q的带正电粒子,其重力不计,从电场的边界MN上的a点由静止释放,经电场加速后进人磁场,穿过中间磁场所用的时间t0=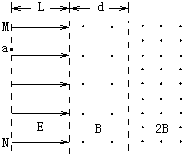 如图所示,水平方向的匀强电场的场强为E,电场区宽度为L,竖直方向足够长,紧挨着电场的是垂直纸面向外的两个匀强磁场区域,其磁感应强度分别为B和2B.一个质量为m、电量为q的带正电的粒子(不计重力)从电场的边界MN上的a点由静止释放,经电场加速后进入磁场,经过tB=πm/4qB 时间穿过中间磁场,进入右边磁场,然后按某一路径再返回到电场的边界MN上的某一点b(虚线为场区的分界面),求:
如图所示,水平方向的匀强电场的场强为E,电场区宽度为L,竖直方向足够长,紧挨着电场的是垂直纸面向外的两个匀强磁场区域,其磁感应强度分别为B和2B.一个质量为m、电量为q的带正电的粒子(不计重力)从电场的边界MN上的a点由静止释放,经电场加速后进入磁场,经过tB=πm/4qB 时间穿过中间磁场,进入右边磁场,然后按某一路径再返回到电场的边界MN上的某一点b(虚线为场区的分界面),求: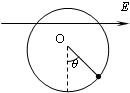 如图所示,水平方向的匀强电场中,有一质量为m的带电小球,用长为l的细线悬于点O,当小球平衡时,细线和竖直方向的夹角为θ,现给小球一个初速度,速度方向和细线垂直,使小球恰能在竖直平面内做圆周运动,则圆周运动过程中速度的最小值为( )
如图所示,水平方向的匀强电场中,有一质量为m的带电小球,用长为l的细线悬于点O,当小球平衡时,细线和竖直方向的夹角为θ,现给小球一个初速度,速度方向和细线垂直,使小球恰能在竖直平面内做圆周运动,则圆周运动过程中速度的最小值为( )