题目内容
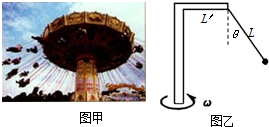图甲为游乐场的悬空旋转椅，我们把这种情况抽象为图乙的模型：一质量m=40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上，水平杆长L′=7.5m．整个装置绕竖直杆转动，绳子与竖直方向成θ角．当θ=37°时，（g=9.8m/s2，sin37°=0.6，cos37°=0.8）求：（1）绳子的拉力大小；
（2）该装置转动的角速度．
分析：（1）球在水平面内做匀速圆周运动，由重力mg和绳的拉力F的合力提供向心力，球在竖直方向力平衡，求解绳的拉力大小．
（2）半径r=Lsin37°+L′，由牛顿第二定律求解角速度．
（2）半径r=Lsin37°+L′，由牛顿第二定律求解角速度．
解答：解：（1）对球受力分析如图所示，
球在竖直方向力平衡，故F拉cos37°=mg；
则：F拉=
；
代入数据得F拉=490N
（2）小球做圆周运动的向心力由绳拉力和重力的合力提供，故：mgtan37°=mω2（Lsin37°+L′）
解得：ω=
=0.7rad/s
答：（1）绳子的拉力大小为490N；
（2）该装置转动的角速度为0.7rad/s．
球在竖直方向力平衡，故F拉cos37°=mg；
则：F拉=
| mg |
| cos37° |
代入数据得F拉=490N
（2）小球做圆周运动的向心力由绳拉力和重力的合力提供，故：mgtan37°=mω2（Lsin37°+L′）
解得：ω=
|
答：（1）绳子的拉力大小为490N；
（2）该装置转动的角速度为0.7rad/s．
点评：本题是圆锥摆问题，关键分析小球的受力情况和运动情况，容易出错的地方是圆周运动的半径r=Lsin37°+L′．
练习册系列答案
走进文言文系列答案
相关题目
角。当θ =37°时，（g = 9.8m/s2，sin37°= 0.6，cos37°= 0.8）求：
角。当θ =37°时，（g = 9.8m/s2，sin37°= 0.6，cos37°= 0.8）求：
角。当θ =37°时，（g = 9.8m/s2，sin37°= 0.6，cos37°= 0.8）求：